Advertisements
Advertisements
प्रश्न
If two opposite vertices of a square are (5, 4) and (1, −6), find the coordinates of its remaining two vertices.
उत्तर
The distance d between two points `(x_1,y_1)` and `(x_2,y_2)` is given by `the formula
`d= sqrt((x_1- x_2)^2+(y_1 -y_2)^2)`
In a square, all the sides are of equal length. The diagonals are also equal to each other. Also in a square, the diagonal is equal to `sqrt2` times the side of the square.
Here let the two points which are said to be the opposite vertices of a diagonal of a square be A(5,4) and C(1,−6).
Let us find the distance between them which is the length of the diagonal of the square.
`AC = sqrt((5 - 1)^2 + (4 = 6)^2)`
`=sqrt((4)^2 + (10)^2)`
`= sqrt(16 + 100)`
`AC = 2sqrt29`
Now we know that in a square,
Side of the square = `"Diagonal of the square"/sqrt2`
Substituting the value of the diagonal we found out earlier in this equation we have,
Side of the square = `(2sqrt29)/sqrt2`
side of the square = `sqrt58`
Now, a vertex of a square has to be at equal distances from each of its adjacent vertices.
Let P(x, y) represent another vertex of the same square adjacent to both ‘A’ and ‘C
`AP = sqrt((5 - x)^2 + (4 - y)^2)`
`CP = sqrt((1 - x)^2 + (-6-y)^2)`
But these two are nothing but the sides of the square and need to be equal to each other.
AP = CP
`sqrt((5 - x)^2 + (4 - y)) = sqrt((1 - x)^2 + (-6 - y)^2)`
Squaring on both sides we have,
`(5 -x)^2 + (4 - y)^2 = (1 - x)^2 + (-6 - y)^2`
`25 + x^2 - 10x + 16 + y^2 - 8y = 1 + x^2 - 2x + 36 + y^2 + 12y`
8x + 20y = 4
2x + 5y = 1
From this we have, x = `(1- 5y)/2`
Substituting this value of ‘x’ and the length of the side in the equation for ‘AP’ we have,
`AP = sqrt((5 - x)^2 + (4 - y)^2)`
`sqrt(58) = sqrt((5 - x)^2 + (4 - y)^2)`
Squaring on both sides,
`58 = (5 - x)^2 + (4 - y)^2`
`58 = (5 - ((1 - 5y)/2))^2 + (4 - y)^2`
`58 = ((9 + 5y)/2)^2 + (4 - y)^2`
`58 = (81 + 25y^2 + +90y)/4 + 16 + y^2 - 8y`
`232 = 81 + 25y^2 + 90y + 64 + 4y^2 - 32y`
`87 = 29y^2 + 58y`
We have a quadratic equation. Solving for the roots of the equation we have,
`29y^2 + 58y - 87 = 0`
`29y^2 + 87y - 29y - 87 = 0`
29y(y + 3) - 29(y + 3) = 0
(y + 3)(29y - 29) = 0
(y + 3)(y - 1) = 0
The roots of this equation are −3 and 1.
Now we can find the respective values of ‘x’ by substituting the two values of ‘y’
When y = -3
`x = (1 - 5(-3))/2`
`= (1 + 15)/2`
x= 8
when y = 1
`x = (1- 5(1))/2`
`= (1-5)/2`
x = -2
Therefore the other two vertices of the square are (8, -3) and (-2, 1).
APPEARS IN
संबंधित प्रश्न
Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right-angled isosceles triangle.
Find the third vertex of a triangle, if two of its vertices are at (−3, 1) and (0, −2) and the centroid is at the origin.
Find the coordinates of the point which divides the line segment joining (−1,3) and (4, −7) internally in the ratio 3 : 4
In what ratio is the line segment joining (-3, -1) and (-8, -9) divided at the point (-5, -21/5)?
If the poin A(0,2) is equidistant form the points B (3, p) and C (p ,5) find the value of p. Also, find the length of AB.
Show that the points A(3,0), B(4,5), C(-1,4) and D(-2,-1) are the vertices of a rhombus. Find its area.
ABCD is a rectangle whose three vertices are A(4,0), C(4,3) and D(0,3). Find the length of one its diagonal.
Find the centroid of ΔABC whose vertices are A(2,2) , B (-4,-4) and C (5,-8).
Find the possible pairs of coordinates of the fourth vertex D of the parallelogram, if three of its vertices are A(5, 6), B(1, –2) and C(3, –2).
If points Q and reflections of point P (−3, 4) in X and Y axes respectively, what is QR?
The distance between the points (a cos 25°, 0) and (0, a cos 65°) is
The perimeter of the triangle formed by the points (0, 0), (0, 1) and (0, 1) is
If three points (0, 0), \[\left( 3, \sqrt{3} \right)\] and (3, λ) form an equilateral triangle, then λ =
If the points (k, 2k), (3k, 3k) and (3, 1) are collinear, then k
If the area of the triangle formed by the points (x, 2x), (−2, 6) and (3, 1) is 5 square units , then x =
If P(2, 4), Q(0, 3), R(3, 6) and S(5, y) are the vertices of a parallelogram PQRS, then the value of y is
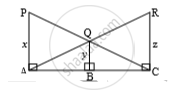
In the above figure, seg PA, seg QB and RC are perpendicular to seg AC. From the information given in the figure, prove that: `1/x + 1/y = 1/z`
Find the coordinates of point A, where AB is a diameter of the circle with centre (–2, 2) and B is the point with coordinates (3, 4).
Point (–10, 0) lies ______.
If the vertices of a parallelogram PQRS taken in order are P(3, 4), Q(–2, 3) and R(–3, –2), then the coordinates of its fourth vertex S are ______.
