Advertisements
Advertisements
प्रश्न
Find the possible pairs of coordinates of the fourth vertex D of the parallelogram, if three of its vertices are A(5, 6), B(1, –2) and C(3, –2).
उत्तर १

ABCD is a parallelogram.
∴ AD = BC and CD = AB ...(Opposite sides of the parallelogram is congruent.)
∴ AD = BC
∴ `sqrt((a - 5)^2 + (b - 6)^2) = sqrt((3 - 1)^2 + [- 2 - (-2)]^2)` ...(Distance Formula)
Squaring bothe the sides,
∴ (a - 5)2 + (b - 6)2 = (3 - 1)2 + (- 2 + 2)2
∴ a2 - 10a + 25 + b2 - 12b + 36 = 4 + 0
∴ a2 + b2 - 10a - 12b + 57 = 0 ...(I)
∴ CD = AB
`∴ sqrt((a - 3)^2 + [b - (- 2)]^2) = sqrt((5 - 1)^2 + [6 - (-2)]^2)` ...(Distance Formula)
Squaring bothe the sides,
∴ (a - 3)2 + (b + 2)2 = (5 - 1)2 + (6 + 2)2
∴ a2 - 6a + 9 + b2 + 4b + 4 = 16 + 64
∴ a2 - 6a + b2 + 4b = 80 - 9 - 4
∴ a2 + b2 - 6a + 4b - 67 = 0 ...(II)
Point D lies on the line passing through the point A. So, the ordinate of the point D will also be same as that of point A which is 6. So, b = 6.
Putting the value of b in (I), we get,
a2 + 62 - 10a - 12 × 6 + 57 = 0
a2 + 36 - 10a - 72 + 57 = 0
a2 - 10a - 21 = 0
a2 - 7a - 3a + 21 = 0
a(a - 7) - 3(a - 7) = 0
(a - 7)(a - 3) = 0
a = 3, 7
Thus, the possible values of point D are (3, 6) and (7, 6).
उत्तर २
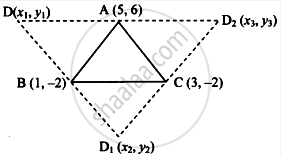
Let the points A(5, 6), B(1, -2) and C(3, -2) be the three vertices of a parallelogram.
The fourth vertex can be point D or point D1 or point D2 as shown in the figure.
Let D(x1, y1), D1(x2, y2) and D2(x3, y3).
Consider the parallelogram ACBD.
The diagonals of a parallelogram bisect each other.
∴ midpoint of DC = midpoint of AB
`∴ ((x_1 + 3)/2, (y_1 - 2)/2) = ((5 + 1)/2, (6 - 2)/2)`
`∴ ((x_1 + 3)/2, (y_1 - 2)/2) = (6/2, 4/2)`
`∴ (x_1 + 3)/2 = 6/2 and (y_1 - 2)/2 = 4/2`
∴ x1 + 3 = 6 and y1 - 2 = 4
∴ x1 = 3 and y1 = 6
Co-ordinates of point D(x1, y1) are (3, 6).
Consider the parallelogram ABD1C.
The diagonals of a parallelogram bisect each other.
∴ midpoint of AD1 = midpoint of BC
`∴ ((x_2 + 5)/2, (y_2 + 6)/2) = ((3 + 1)/2, (-2 - 2)/2)`
`∴ ((x_2 + 5)/2, (y_2 + 6)/2) = (4/2, (-4)/2)`
`∴ (x_2 + 5)/2 = 4/2 and (y_2 + 6)/2 = (-4)/2`
∴ x2 + 5 = 4 and y2 + 6 = -4
∴ x2 = - 1 and y2 = - 10
∴ Co-ordinates of D (x2, y2) are (-1,-10).
Consider the parallelogram ABCD2.
The diagonals of a parallelogram bisect each other.
∴ midpoint of BD2 = midpoint of AC
`∴ ((x_3 + 1)/2, (y_3 - 2)/2) = ((5 + 3)/2, (6 - 2)/2)`
`∴ ((x_3 + 1)/2, (y_3 - 2)/2) = (8/2, 4/2)`
`∴ (x_3 + 1)/2 = 8/2 and (y_3 - 2)/2 = 4/2`
∴ x3 + 1 = 8 and y3 - 2 = 4
∴ x3 = 7 and y3 = 6
∴ co-ordinates of point D2(x3 , y3) are (7, 6).
∴ The possible pairs of co-ordinates of the fourth vertex D of the parallelogram are (3, 6), (-1, -10) and (7, 6).
APPEARS IN
संबंधित प्रश्न
On which axis do the following points lie?
P(5, 0)
Find the centre of the circle passing through (5, -8), (2, -9) and (2, 1).
If two opposite vertices of a square are (5, 4) and (1, −6), find the coordinates of its remaining two vertices.
Find the coordinates of the point which divides the line segment joining (−1,3) and (4, −7) internally in the ratio 3 : 4
Find the ratio in which the line segment joining (-2, -3) and (5, 6) is divided by x-axis Also, find the coordinates of the point of division in each case.
The points A(2, 0), B(9, 1) C(11, 6) and D(4, 4) are the vertices of a quadrilateral ABCD. Determine whether ABCD is a rhombus or not.
If the coordinates of the mid-points of the sides of a triangle be (3, -2), (-3, 1) and (4, -3), then find the coordinates of its vertices.
Points P, Q, R and S divide the line segment joining the points A(1,2) and B(6,7) in five equal parts. Find the coordinates of the points P,Q and R
Find the area of quadrilateral PQRS whose vertices are P(-5, -3), Q(-4,-6),R(2, -3) and S(1,2).
A point whose abscissa and ordinate are 2 and −5 respectively, lies in
Show that the points (−4, −1), (−2, −4) (4, 0) and (2, 3) are the vertices points of a rectangle.
If the point \[C \left( - 1, 2 \right)\] divides internally the line segment joining the points A (2, 5) and B( x, y ) in the ratio 3 : 4 , find the value of x2 + y2 .
If the distance between the points (3, 0) and (0, y) is 5 units and y is positive. then what is the value of y?
If points (t, 2t), (−2, 6) and (3, 1) are collinear, then t =
Find the point on the y-axis which is equidistant from the points (S, - 2) and (- 3, 2).
The line segment joining the points A(2, 1) and B (5, - 8) is trisected at the points P and Q such that P is nearer to A. If P also lies on the line given by 2x - y + k= 0 find the value of k.
The distance of the point P(2, 3) from the x-axis is ______.
Abscissa of all the points on the x-axis is ______.
Statement A (Assertion): If the coordinates of the mid-points of the sides AB and AC of ∆ABC are D(3, 5) and E(–3, –3) respectively, then BC = 20 units.
Statement R (Reason): The line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half of it.
The distance of the point (–4, 3) from y-axis is ______.
