Advertisements
Advertisements
प्रश्न
Find the possible pairs of coordinates of the fourth vertex D of the parallelogram, if three of its vertices are A(5, 6), B(1, –2) and C(3, –2).
उत्तर १

ABCD is a parallelogram.
∴ AD = BC and CD = AB ...(Opposite sides of the parallelogram is congruent.)
∴ AD = BC
∴ `sqrt((a - 5)^2 + (b - 6)^2) = sqrt((3 - 1)^2 + [- 2 - (-2)]^2)` ...(Distance Formula)
Squaring bothe the sides,
∴ (a - 5)2 + (b - 6)2 = (3 - 1)2 + (- 2 + 2)2
∴ a2 - 10a + 25 + b2 - 12b + 36 = 4 + 0
∴ a2 + b2 - 10a - 12b + 57 = 0 ...(I)
∴ CD = AB
`∴ sqrt((a - 3)^2 + [b - (- 2)]^2) = sqrt((5 - 1)^2 + [6 - (-2)]^2)` ...(Distance Formula)
Squaring bothe the sides,
∴ (a - 3)2 + (b + 2)2 = (5 - 1)2 + (6 + 2)2
∴ a2 - 6a + 9 + b2 + 4b + 4 = 16 + 64
∴ a2 - 6a + b2 + 4b = 80 - 9 - 4
∴ a2 + b2 - 6a + 4b - 67 = 0 ...(II)
Point D lies on the line passing through the point A. So, the ordinate of the point D will also be same as that of point A which is 6. So, b = 6.
Putting the value of b in (I), we get,
a2 + 62 - 10a - 12 × 6 + 57 = 0
a2 + 36 - 10a - 72 + 57 = 0
a2 - 10a - 21 = 0
a2 - 7a - 3a + 21 = 0
a(a - 7) - 3(a - 7) = 0
(a - 7)(a - 3) = 0
a = 3, 7
Thus, the possible values of point D are (3, 6) and (7, 6).
उत्तर २
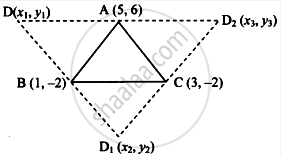
Let the points A(5, 6), B(1, -2) and C(3, -2) be the three vertices of a parallelogram.
The fourth vertex can be point D or point D1 or point D2 as shown in the figure.
Let D(x1, y1), D1(x2, y2) and D2(x3, y3).
Consider the parallelogram ACBD.
The diagonals of a parallelogram bisect each other.
∴ midpoint of DC = midpoint of AB
`∴ ((x_1 + 3)/2, (y_1 - 2)/2) = ((5 + 1)/2, (6 - 2)/2)`
`∴ ((x_1 + 3)/2, (y_1 - 2)/2) = (6/2, 4/2)`
`∴ (x_1 + 3)/2 = 6/2 and (y_1 - 2)/2 = 4/2`
∴ x1 + 3 = 6 and y1 - 2 = 4
∴ x1 = 3 and y1 = 6
Co-ordinates of point D(x1, y1) are (3, 6).
Consider the parallelogram ABD1C.
The diagonals of a parallelogram bisect each other.
∴ midpoint of AD1 = midpoint of BC
`∴ ((x_2 + 5)/2, (y_2 + 6)/2) = ((3 + 1)/2, (-2 - 2)/2)`
`∴ ((x_2 + 5)/2, (y_2 + 6)/2) = (4/2, (-4)/2)`
`∴ (x_2 + 5)/2 = 4/2 and (y_2 + 6)/2 = (-4)/2`
∴ x2 + 5 = 4 and y2 + 6 = -4
∴ x2 = - 1 and y2 = - 10
∴ Co-ordinates of D (x2, y2) are (-1,-10).
Consider the parallelogram ABCD2.
The diagonals of a parallelogram bisect each other.
∴ midpoint of BD2 = midpoint of AC
`∴ ((x_3 + 1)/2, (y_3 - 2)/2) = ((5 + 3)/2, (6 - 2)/2)`
`∴ ((x_3 + 1)/2, (y_3 - 2)/2) = (8/2, 4/2)`
`∴ (x_3 + 1)/2 = 8/2 and (y_3 - 2)/2 = 4/2`
∴ x3 + 1 = 8 and y3 - 2 = 4
∴ x3 = 7 and y3 = 6
∴ co-ordinates of point D2(x3 , y3) are (7, 6).
∴ The possible pairs of co-ordinates of the fourth vertex D of the parallelogram are (3, 6), (-1, -10) and (7, 6).
APPEARS IN
संबंधित प्रश्न
On which axis do the following points lie?
P(5, 0)
Find the distance between the following pair of points:
(a, 0) and (0, b)
Two vertices of an isosceles triangle are (2, 0) and (2, 5). Find the third vertex if the length of the equal sides is 3.
The line segment joining the points P(3, 3) and Q(6, -6) is trisected at the points A and B such that Ais nearer to P. If A also lies on the line given by 2x + y + k = 0, find the value of k.
Determine the ratio in which the point (-6, a) divides the join of A (-3, 1) and B (-8, 9). Also, find the value of a.
Find the co-ordinates of the point equidistant from three given points A(5,3), B(5, -5) and C(1,- 5).
If the point A (4,3) and B ( x,5) lies on a circle with the centre o (2,3) . Find the value of x.
Find the point on x-axis which is equidistant from points A(-1,0) and B(5,0)
Show that A(-4, -7), B(-1, 2), C(8, 5) and D(5, -4) are the vertices of a
rhombus ABCD.
The distance of the point P (4, 3) from the origin is
Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles.
If the point P (m, 3) lies on the line segment joining the points \[A\left( - \frac{2}{5}, 6 \right)\] and B (2, 8), find the value of m.
what is the value of \[\frac{a^2}{bc} + \frac{b^2}{ca} + \frac{c^2}{ab}\] .
If the points A (1,2) , O (0,0) and C (a,b) are collinear , then find a : b.
The perimeter of the triangle formed by the points (0, 0), (0, 1) and (0, 1) is
If points (t, 2t), (−2, 6) and (3, 1) are collinear, then t =
The coordinates of a point on x-axis which lies on the perpendicular bisector of the line segment joining the points (7, 6) and (−3, 4) are
Find the coordinates of the point whose ordinate is – 4 and which lies on y-axis.
If the coordinate of point A on the number line is –1 and that of point B is 6, then find d(A, B).
Ryan, from a very young age, was fascinated by the twinkling of stars and the vastness of space. He always dreamt of becoming an astronaut one day. So, he started to sketch his own rocket designs on the graph sheet. One such design is given below :
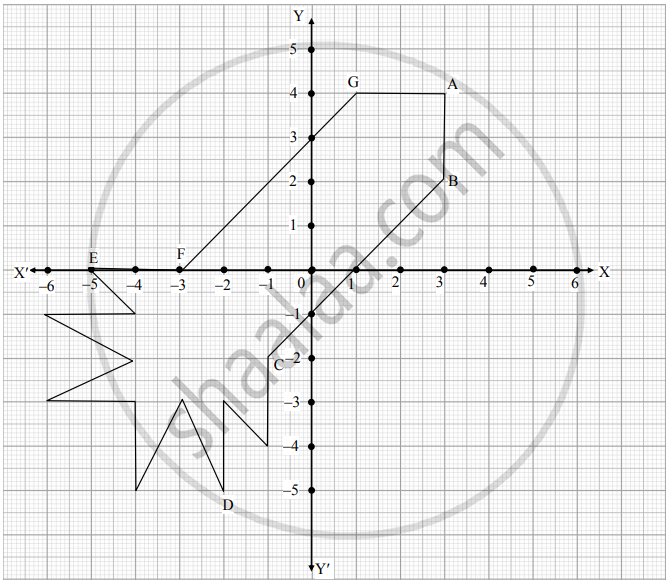
Based on the above, answer the following questions:
i. Find the mid-point of the segment joining F and G. (1)
ii. a. What is the distance between the points A and C? (2)
OR
b. Find the coordinates of the points which divides the line segment joining the points A and B in the ratio 1 : 3 internally. (2)
iii. What are the coordinates of the point D? (1)
