Advertisements
Advertisements
Question
In the given figure, PQ || RS. If ∠1 = (2a + b)° and ∠6 = (3a – b)°, then the measure of ∠2 in terms of b is ______.
Options
(2 + b)°
(3 – b)°
(108 – b)°
(180 – b)°
Solution
In figure, PQ || RS. If ∠1 = (2a + b)° and ∠6 = (3a – b)°, then the measure of ∠2 in terms of b is (108 – b)°.
Explanation:

Since, PQ || RS and line 1 is a transversal.
∴ ∠2 = ∠6 = (34 – b)° ......(i) [Corresponding angles]
∠1 + ∠2 = 180° ......[Angles on a straight line PQ]
⇒ ∠2 = 180° – (2a+ b)° ......(ii) [∵ ∠1 = (2a + b)° (given)]
From (i) and (ii), we have
⇒ (3a – b)° = 180° – (2a + b)°
⇒ 3a – b = 180 – 2a – b
⇒ 3a – b + 2a + b = 180
⇒ 5a = 180
⇒ a = `180/5` = 36
∴ a = 36
Now, ∠2 – (3a – b)° ......[From (i)]
⇒ ∠2 = (3 × 36 – b)° = (108 – b)°
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
Two angles forming a linear pair are ______

If the three angles at a point are in the ratio 1 : 4 : 7, find the value of each angle?
In the given figure the angles ∠1 and ∠2 are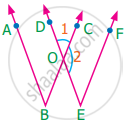
Angles between South and West and South and East are ______.
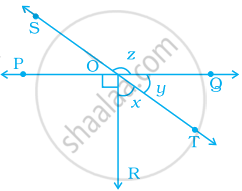
In the given figure, lines PQ and ST intersect at O. If ∠POR = 90° and x:y = 3:2, then z is equal to ______.
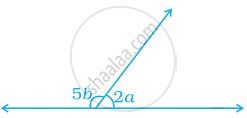
In the given figure, a = 40°. The value of b is ______.
Two supplementary angles always form a linear pair.
What is the type of other angle of a linear pair if one of its angles is right?
