Advertisements
Advertisements
Question
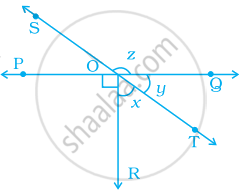
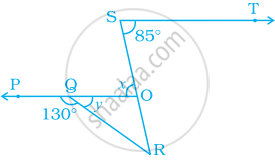
In the given figure, lines PQ and ST intersect at O. If ∠POR = 90° and x:y = 3:2, then z is equal to ______.
Options
126°
144°
136°
154°
Solution
In the given figure, lines PQ and ST intersect at O. If ∠POR = 90° and x:y = 3:2, then z is equal to 144°.
Explanation:

Since, ∠POR, ∠ROT and ∠TOQ lie on a straight line POQ, then their sum is equal to 180°.
∴ ∠POR + ∠ROT + ∠TOQ = 180°
⇒ 90° + x + y = 180°
⇒ x + y = 180° – 90°
⇒ x + y = 90° ......(i)
Also, x:y = 3:2 ......[Given]
Let x = 3a and y = 2a
∴ 3a + 2a = 90° ......[From equation (i)]
⇒ 5a = 90°
⇒ a = `90^circ/5` = 18°
Now, x = 3a = 3 × 18° = 54° and y = 2a = 2 × 18° = 36°
Since, y and z form a linear pair
∴ y + z = 180°
⇒ 36° + z = 180°
⇒ z = 180° – 36° ......[∵ y = 36°]
⇒ z = 144°
APPEARS IN
RELATED QUESTIONS
Indicate which pairs of angles are: Linear pairs.

Are the ray PM and PT opposite rays? Give reasons for your answer.

The measure of ∠BOC is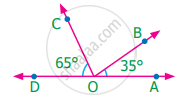
Using the figure, answer the following question and justify your answer
Does ∠BOC and ∠BOD form a linear pair?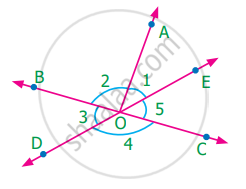
In the given figure, PQ || RS. If ∠1 = (2a + b)° and ∠6 = (3a – b)°, then the measure of ∠2 in terms of b is ______.
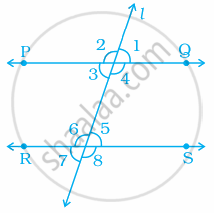
In the given figure, PQ || ST. Then, the value of x + y is ______.
Two angles making a linear pair are always supplementary.
What is the type of other angle of a linear pair if one of its angles is right?
