Advertisements
Advertisements
Question
In order to stop a car in shortest distance on a horizontal road, one should
Options
apply the brakes very hard so that the wheels stop rotating
apply the brakes hard enough to just prevent slipping
pump the brakes (press and release)
shut the engine off and not apply brakes
Solution
apply the brakes hard enough to just prevent slipping
When we apply hard brakes just enough to prevent slipping on wheels, it provides optimum normal reaction force, which gives the maximum friction force between tyres of the car and the road.
APPEARS IN
RELATED QUESTIONS
Can you accelerate a car on a frictionless horizontal road by putting more petrol in the engine? Can you stop a car going on a frictionless horizontal road by applying brakes?
A scooter starting from rest moves with a constant acceleration for a time ∆t1, then with a constant velocity for the next ∆t2 and finally with a constant deceleration for the next ∆t3 to come to rest. A 500 N man sitting on the scooter behind the driver manages to stay at rest with respect to the scooter without touching any other part. The force exerted by the seat on the man is
Two cars of unequal masses use similar tyres. If they are moving at the same initial speed, the minimum stopping distance
Consider a vehicle going on a horizontal road towards east. Neglect any force by the air. The frictional force on the vehicle by the road
(a) is towards east if the vehicle is accelerating
(b) is zero if the vehicle is moving with a uniform velocity
(c) must be towards east
(d) must be towards west.
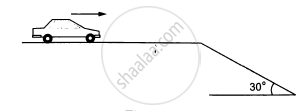
A care is going at a speed of 21.6 km/hr when it encounters at 12.8 m long slope of angle 30° (in the following figure). The friction coefficient between the road and the tyre is `1/2sqrt3`. Show that no matter how hard the driver applies the brakes, the car will reach the bottom with a speed greater than 36 km/hr. Take g = 10 m/s2.
A car starts from rest on a half kilometre long bridge. The coefficient of friction between the tyre and the road is 1.0. Show that one cannot drive through the bridge in less than 10 s.
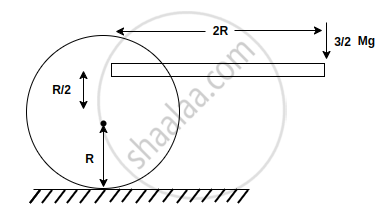
A disc of mass M and radius R is placed a rough horizontal surface with its axis horizontal. A light rod of length '2R' is fixed to the disc at point 'A' as shown in figure and a force `3/2` Mg is applied at the other end. If disc starts to roll without slipping the value of "10 × µmin" where µmin is minimum coefficient of friction between disc and horizontal surface required for pure rolling is ______.