Question

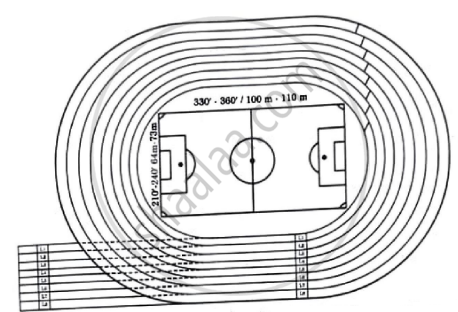
In order to organise, Annual sports Day, a school prepared an eight-lane running track with an integrated football field inside the track area as shown below: The length of innermost lane of the track is 400 m and each subsequent lane is 7.6 m longer than the preceding lane. Based on given information, answer the following questions, using concept of Arithmetic Progression.

1. What is the length of the 6^th lane?   [1]
2. How long is the 8^th lane than that of 4^th lane?   [1]
3. 
   
   1. While practicing for a race, a student took one round each in first six lanes. Find the total distance covered by the student.   [2]
                                         OR
   2. A student took one round each in lane 4 to lane 8. Find the total distance covered by the student.    [2]

Answer 1

i. a_n ​= a + (n − 1)d

For the 6^th lane (n = 6):

a₆ ​= 400 + (6 − 1) × 7.6

= 400 + 5 × 7.6

= 400 + 38

= 438 m

So, the length of the 6^th lane is 438 m.

ii. For the 8^th lane (n = 8):

a₈ ​= 400 + (8 − 1) × 7.6

= 400 + 7 × 7.6

= 400 + 53.2

= 453.2 m

For the 4^th lane (n = 4):

a₄ ​= 400 + (4 − 1) × 7.6

= 400 + 3 × 7.6

= 400 + 22.8

= 422.8 m

Difference:

453.2 − 422.8 

= 30.4 m

So, the 8^th lane is 30.4 m longer than the 4^th lane.

iii. (a) S_n = `n/2[2a + (n - 1)d]`

For n = 6

S₆ = `6/2[2(400) + (6 - 1)×7.6]`

= 3[800 + 38]

= 3 × 838

= 2514 m

So, the total distance covered by the student is 2514 m.

OR

iii. (b) We sum the terms from 4^th lane to 8^th lane.

Using the sum formula for n terms, where a₄ to a₈​ are considered:

S_n = `n/2[2a+(n-1)d]`

Here, n = 5 (as we consider lanes 4, 5, 6, 7, and 8).

S₅ = `5/2[2(422.8)+(5-1)xx7.6]`

= `5/2[845.6+30.4]`

= `5/2xx876`

= `4380/2`

= 2190 m

So, the total distance covered by the student is 2190 m.