English Medium
Academic Year: 2024-2025
Date & Time: 10th March 2025, 10:30 am
Duration: 3h
Advertisements
General Instructions:
- This question paper contains 38 questions.
All questions are compulsory. - This Question Paper is divided into FIVE Sections - Section A, B, C, D, and E.
- In Section - A question number 1 to 18 are Multiple Choice Questions (MCQs) and question number 19 & 20 are Assertion Reason based question of 1 mark each.
- In Section - B questions number 21 to 25 are Very Short-Answer-I (SA-I) type questions of 2 marks each.
- In Section - C questions number 26 to 31 are Short Answer-II (SA-II) type questions carrying 3 marks each.
- In Section - D questions number 32 to 35 are Long Answer (LA) type questions carrying 5 marks each.
- In Section - E questions number 36 to 38 are Case Study/Passage based integrated units and assessment questions carrying 4 marks each. Internal choice is provided in 2 marks questions in each case study.
- There is no overall choice. However, an internal choice has been provided in 2 questions in Section - B, 2 questions in Section - C, 2 questions in Section - D, and 3 questions in Section - E.
- Draw neat figures wherever required. Take π = `22/7` wherever required if not stated.
- Use of a calculator is NOT allowed.
`sqrt0.4` is a/an ______.
natural number
integer
rational number
irrational number
Chapter:
Which of the following cannot be the unit digit of 8n, where n is a natural number?
4
2
0
6
Chapter:
Which of the following quadratic equations has real and equal roots?
(x + 1)2 = 2x + 1
x2 + x = 0
x2 − 4 = 0
x2 + x + 1 = 0
Chapter:
If the zeroes of the polynomial `ax^2+bx+(2a)/b` are reciprocal of each other, then the value of b is ______.
2
`1/2`
−2
`-1/2`
Chapter:
The distance of the point A(−3, −4) from x-axis is ______.
3
4
5
7
Chapter:
In the adjoining figure, PQ || XY || BC, AP = 2 cm, PX = 1.5 cm and BX = 4 cm. If QY = 0.75 cm, then AQ + CY = ______.
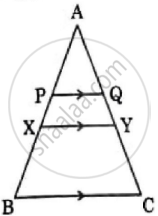
6 cm
4.5 cm
3 cm
5.25 cm
Chapter:
Given ΔABC ~ ΔPQR, ∠A = 30° ∠Q = 90°. The value of (∠R + ∠B) is ______.
90°
120°
150°
180°
Chapter:
Two coins are tossed simultaneously. The probability of getting atleast one head is ______.
`1/4`
`1/2`
`3/4`
1
Chapter:
In the adjoining figure, PA and PB are tangents to a circle with centre O such that ∠P = 90°. If AB = `3sqrt2` cm, then the diameter of the circle is ______.
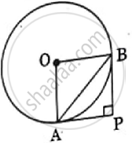
`3sqrt2` cm
`6sqrt2` cm
3 cm
6 cm
Chapter:
For a circle with centre O and radius 5 cm, which of the following statements is true?
- P: Distance between every pair of parallel tangents is 5 cm.
- Q: Distance between every pair of parallel tangents is 10 cm.
- R: Distance between every pair of parallel tangents must be between 5 cm and 10 cm.
- S: There does not exist a point outside the circle from where length of tangent is 5 cm.
P
Q
R
S
Chapter:
In the adjoining figure, TS is a tangent to a circle with centre O. The value of 2x° is ______.
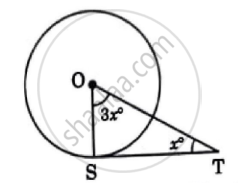
22.5
45
67.5
90
Chapter:
If x `((2tan30°)/(1+tan^2 30°)) = y((2tan30°)/(1-tan^2 30°))`, then x : y = ______.
1 : 1
1 : 2
2 : 1
4 : 1
Chapter:
A peacock sitting on the top of a tree of height 10 m observes a snake moving on the ground. If the snake is `10sqrt3` m away from the base of the tree, then angle of depression of the snake from the eye of the peacock is ______.
30°
45°
60°
90°
Chapter:
If a cone of greatest possible volume is hollowed out from a solid wooden cylinder. We need to find the ratio of the volume of remaining wood to the volume of the cone hollowed out is ______.
1:1
1:3
2:1
3:1
Chapter:
If the mode of some observations is 10 and sum of mean and median is 25, then the mean and median, respectively, are ______.
12 and 13
13 and 12
10 and 15
15 and 10
Chapter:
If the maximum number of students has obtained 52 marks out of 80, then ______.
52 is the mean of the data.
52 is the median of the data.
52 is the mode of the data.
52 is the range of the data.
Chapter:
Advertisements
The system of equations 2x + 1 = 0 and 8y − 5 = 0 has ______.
unique solution
two solutions
no solution
infinite number of solutions
Chapter:
In a right triangle ABC, right-angled at A, if sin B = `1/4`, then the value of sec B is ______.
4
`sqrt15/4`
`sqrt15`
`4/sqrt15`
Chapter:
Assertion (A): For any two prime numbers p and q, their HCF is 1 and LCM is p + q.
Reason (R): For any two natural numbers, HCF × LCM = product of numbers.
Both Assertion (A) and Reason (R) are true and Reason (R) is correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Chapter:
In an experiment of throwing a die,
Assertion (A): Event E1: getting a number less than 3, and Event E2 : getting a number greater than 3 are complementary events.
Reason (R): If two events E and F are complementary events, then P(E) + P(F) = 1
Both Assertion (A) and Reason (R) are true, and Reason (R) is a correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
Chapter:
Solve the following pair of equations algebraically:
101x + 102y = 304
102x + 101y = 305
Chapter:
In a pair of supplementary angles, the greater angle exceeds the smaller by 50°. Express the given situation as a system of linear equations in two variables and hence obtain the measure of each angle.
Chapter:
If a sec θ + b tan θ = m and b sec θ + a tan θ = n, prove that a2 + n2 = b2 + m2
Chapter:
Use the identity: sin2A + cos2A = 1 to prove that tan2A + 1 = sec2A. Hence, find the value of tan A, when sec A = `5/3`, where A is an acute angle.
Chapter:
Prove that abscissa of a point P which is equidistant from points with coordinates A(7, 1) and B(3, 5) is 2 more than its ordinate.
Chapter:
P is a point on the side BC of ΔABC such that ∠APC = ∠BAC. Prove that AC2 = BC·CP.
Chapter:
The number of red balls in a bag is three more than the number of black balls. If the probability of drawing a red ball at random from the given bag is `12/23`, find the total number of balls in the given bag.
Chapter:
Prove that `sqrt(5)` is an irrational number.
Chapter: [0.011000000000000001] Real Numbers
Let p, q and r be three distinct prime numbers.
Check whether p.q.r + q is a composite number or not.
Further, give an example for 3 distinct primes p, q, r such that
- P.q.r + 1 is a composite number.
- P.q.r + 1 is a prime number.
Chapter:
Advertisements
Find the zeroes of the polynomial p(x) = 3x2 − 4x − 4. Hence, write a polynomial whose each of the zeroes is 2 more than the zeroes of p(x).
Chapter:
Check whether the following pair of equations is consistent or not. If consistent, solve graphically:
x + 3y = 6
3y − 2x = −12
Chapter:
If the points A(6, 1), B(p, 2), C(9, 4) and D(7, 9) are the vertices of a parallelogram ABCD, then find the values of p and g. Hence, check whether ABCD is a rectangle or not.
Chapter:
Prove that: `(cos theta - 2 cos^3 theta)/(sin theta - 2 sin^3 theta) + cot theta = 0`.
Chapter:
Given that sin θ + cos θ = x, prove that sin4 θ + cos4 θ = `(2-(x^2-1)^2)/2`.
Chapter:
In the adjoining figure, TP and TQ are tangents drawn to a circle with centre O. If ∠OPQ = 15° and ∠PTQ = θ, then find the value of sin 2θ.
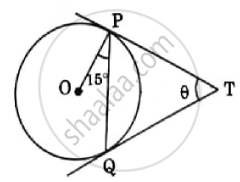
Chapter:
There is a circular park of diameter 65 m as shown in the following figure, where AB is a diameter.
An entry gate is to be constructed at the point P on the boundary of the park such that distance of P from A is 35 m more than the distance of P from B. Find the distance of point P from A and B, respectively.
Chapter:
Find the smallest value of p for which the quadratic equation x2 − 2(p + 1)x + p2 = 0 has real roots. Hence, find the roots of the equation so obtained.
Chapter:
If a line drawn parallel to one side of a triangle intersecting the other two sides in distinct points divides the two sides in the same ratio, then it is parallel to the third side.
State and prove the converse of the above statement.
Chapter:
In the adjoining figure, ΔCAB is a right triangle, right angled at A and AD ⊥ BC. Prove that ΔADB ~ ΔCDA. Further, if BC = 10 cm and CD = 2 cm, find the length of AD.

Chapter:
From one face of a solid cube of side 14 cm, the largest possible one is carved out. Find the volume and surface area of the remaining solid. (Use π = `22/7`, `sqrt5 = 2.2`)
Chapter:
Following distribution shows the marks of 230 students in a particular subject. If the median marks are 46, then find the values of x and y.
| Marks | Number of students |
| 10 - 20 | 12 |
| 20 - 30 | 30 |
| 30 - 40 | x |
| 40 - 50 | 65 |
| 50 - 60 | y |
| 60 - 70 | 25 |
| 70 - 80 | 18 |
Chapter:
|
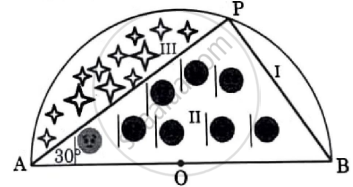
Anurag purchased a farmhouse which is in the form of a semicircle of diameter 70 m. He divides it into three parts by taking a point P on the semicircle in such a way that ∠PAB = 30° as shown in the following figure, where O is the centre of the semicircle.
In part I, he planted saplings of Mango tree, in part II, he grew tomatoes and in part III, he grew oranges. Based on given information, answer the following questions. |
- What is the measure of ∠POA? [1]
- Find the length of wire needed to fence entire piece of land. [1]
-
- Find the area of region in which saplings of Mango tree are planted. [2]
OR - Find the length of wire needed to fence the region III. [2]
- Find the area of region in which saplings of Mango tree are planted. [2]
Chapter:
|
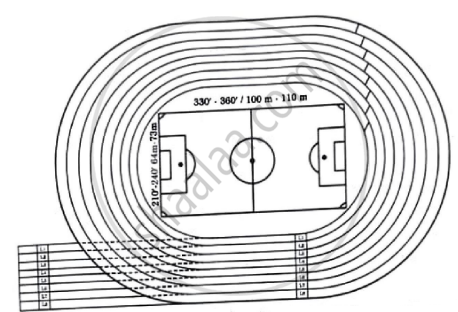
In order to organise, Annual sports Day, a school prepared an eight-lane running track with an integrated football field inside the track area as shown below:
The length of innermost lane of the track is 400 m and each subsequent lane is 7.6 m longer than the preceding lane. Based on given information, answer the following questions, using concept of Arithmetic Progression. |
- What is the length of the 6th lane? [1]
- How long is the 8th lane than that of 4th lane? [1]
- While practicing for a race, a student took one round each in first six lanes. Find the total distance covered by the student. [2]
OR - A student took one round each in lane 4 to lane 8. Find the total distance covered by the student. [2]
- While practicing for a race, a student took one round each in first six lanes. Find the total distance covered by the student. [2]
Chapter:
|
The Statue of Unity situated in Gujarat is the world's largest Statue which stands over a 58 m high base. As part of the project, a student constructed an inclinometer and wishes to find the height of Statue of Unity using it. He noted following observations from two places: Situation − I: The angle of elevation of the top of Statue from Place A which is 80`sqrt3` m away from the base of the Statue is found to be 60°. Situation − II: The angle of elevation of the top of Statue from a Place B which is 40 m above the ground is found to be 30° and entire height of the statue, including the base, is found to be 240 m.
|
Based on the given information, answer the following questions:
- Represent the Situation – I with the help of a diagram. [1]
- Represent the Situation − II with the help of a diagram. [1]
-
- Calculate the height of Statue excluding the base and also find the height including the base with the help of Situation − I. [2]
OR - Find the horizontal distance of point B (Situation - II) from the Statue and the value of tan α, where α is the angle of elevation of the top of the base of the Statue from point B. [2]
- Calculate the height of Statue excluding the base and also find the height including the base with the help of Situation − I. [2]
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2024 - 2025
Previous year Question paper for CBSE Class 10 Maths-2025 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.