Question

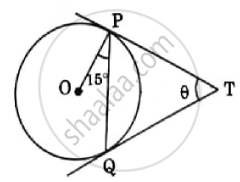
In the adjoining figure, TP and TQ are tangents drawn to a circle with centre O. If ∠OPQ = 15° and ∠PTQ = θ, then find the value of sin 2θ.

Answer 1

Given:

• TP and TQ are tangents to a circle from an external point T.
• ∠OPQ = 15°.
• ∠PTQ = θ.

Find the value of sin 2θ.

Step 1: Find the value of θ 

Since TP and TQ are tangents from an external point, they are equal in length, forming an isosceles triangle △OPT.

We know that the angle subtended by a tangent at the point of contact with the radius is 90°,

∠OPQ = 15°

Since OQ = OP (radii of the circle), ΔOQP is an isosceles triangle and we apply the property:

θ = 2 × ∠OPQ

θ = 2 × 15° = 30°

Step 2: Find sin 2θ 

sin2θ = 2sin θ cos θ

Substituting θ = 30°: sin 2(30°) = sin 60°

sin 60° = `sqrt3/2`

sin 2θ = `sqrt3/2`