Advertisements
Advertisements
Question
In ΔPQR, If PQ > PR and bisectors of ∠Q and ∠R intersect at S. Show that SQ > SR.

Solution
Given: In ΔPQR, PQ > PR and bisectors of ∠Q and ∠R intersect at S.
To prove: SQ > SR
Proof:
∠SQR = `1/2` ∠PQR ...(i) ...[Ray QS bisects ∠PQR]
∠SRQ = `1/2` ∠PRQ ...(ii) ...[Ray RS bisects ∠PRQ]
In ∆PQR,
PQ > PR ...[Given]
∴ ∠R > ∠Q ....[Angle opposite to greater side is greater.]
∴ `1/2 ("∠R") > 1/2 ("∠Q") ...["Multiplying both sides by" 1/2]`
∴ ∠SRQ > ∠SQR ...(iii) ...[From (i) and (ii)]
In ∆SQR,
∠SRQ > ∠SQR ...[From (iii)]
∴ SQ > SR ...[Side opposite to greater angle is greater]
APPEARS IN
RELATED QUESTIONS
In the given figure, point A is on the bisector of ∠ XYZ. If AX = 2 cm then find AZ.


In the given figure, ∠RST = 56°, seg PT ⊥ ray ST, seg PR ⊥ ray SR and seg PR ≅ seg PT. Find the measure of ∠RSP. State the reason for your answer.
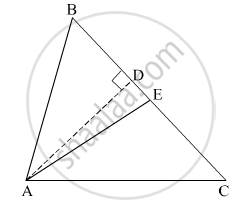
Prove that, if the bisector of ∠BAC of ΔABC is perpendicular to side BC, then ΔABC is an isosceles triangle.
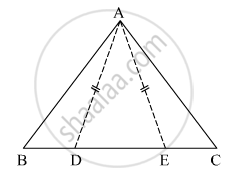
In the figure, point D and E are on side BC of ΔABC, such that BD = CE and AD = AE. Show that ΔABD ≅ ΔACE.
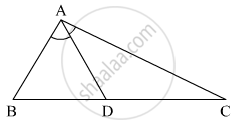
In the given figure, bisector of ∠BAC intersects side BC at point D. Prove that AB > BD.
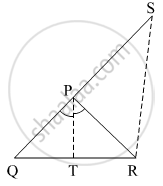
In the given figure, seg PT is the bisector of ∠QPR. A line through R intersects ray QP at point S. Prove that PS = PR.
In the given figure, seg AD ⊥ seg BC. seg AE is the bisector of ∠CAB and C - E - D. Prove that ∠DAE = `1/2` (∠C - ∠B)