Advertisements
Advertisements
Question
Prove that, if the bisector of ∠BAC of ΔABC is perpendicular to side BC, then ΔABC is an isosceles triangle.
Solution
Given: Seg AD is the bisector of ∠BAC. Seg AD ⊥ seg BC.
To prove: ΔABC is an isosceles triangle.
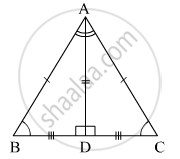
Proof:
In ∆ABD and ∆ACD,
∠BAD ≅ ∠CAD ...[seg AD is the bisector of ∠BAC]
seg AD ≅ seg AD ...[Common side]
∠ADB ≅ ∠ADC ...[Each angle is of measure 90°]
∴ ∆ABD ≅ ∆ACD ...[ASA test]
∴ seg AB ≅ seg AC ...[c. s. c. t.]
∴ ∆ABC is an isosceles triangle.
APPEARS IN
RELATED QUESTIONS
In the given figure, point A is on the bisector of ∠ XYZ. If AX = 2 cm then find AZ.


In the given figure, ∠RST = 56°, seg PT ⊥ ray ST, seg PR ⊥ ray SR and seg PR ≅ seg PT. Find the measure of ∠RSP. State the reason for your answer.
In ΔPQR, If PQ > PR and bisectors of ∠Q and ∠R intersect at S. Show that SQ > SR.

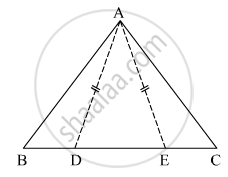
In the figure, point D and E are on side BC of ΔABC, such that BD = CE and AD = AE. Show that ΔABD ≅ ΔACE.
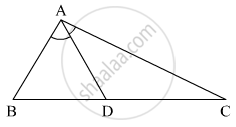
In the given figure, bisector of ∠BAC intersects side BC at point D. Prove that AB > BD.
In the given figure, seg PT is the bisector of ∠QPR. A line through R intersects ray QP at point S. Prove that PS = PR.
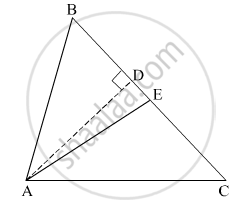
In the given figure, seg AD ⊥ seg BC. seg AE is the bisector of ∠CAB and C - E - D. Prove that ∠DAE = `1/2` (∠C - ∠B)