Advertisements
Advertisements
Question
Prove that an equilateral triangle is equiangular.
Solution
Consider an equilateral triangle ABC.

In △ABC,
AB ≅ BC
∴ ∠ACB = ∠BAC ...(1)...(Angles opposite to equal sides)
In △ABC,
AB ≅ CA
∴ ∠ACB = ∠ABC ...(2)...(Angles opposite to equal sides)
From (1) and (2), we get
∠BAC ≅ ∠ABC ≅ ∠ACB
Hence, an equilateral triangle is equiangular.
APPEARS IN
RELATED QUESTIONS
ΔDEF ~ ΔMNK. If DE = 5, MN = 6, then find the value of `"A(ΔDEF)"/"A(ΔMNK)"`
Select the correct alternative answer and write it.
The ratio of corresponding sides of similar triangles is 5 : 7, then what is
the ratio of their areas ?
(A)25 : 49 (B) 49 : 25 (C) 5 : 7 (D) 7 : 5
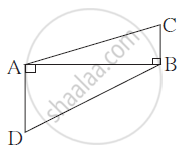
In the given figure, CB ⊥ AB, DA ⊥ AB.
if BC = 4, AD = 8 then `(A(Δ ABC))/(A(Δ ADB))` find.
Δ ABC ∼ Δ PQR. If A(Δ ABC)=25, A(ΔPQR)=16, find AB : PQ.
(A) 25:16
(B) 4:5
(C) 16:25
(D) 5:4
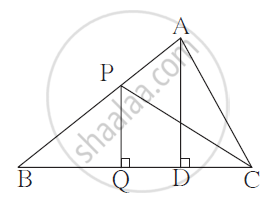
In the adjoining figure,
PQ ⊥ BC, AD ⊥ BC,
PQ = 4, AD = 6
Write down the following ratios.
(i)`(A(ΔPQB))/(A(ΔADB))`
(ii)`(A(ΔPBC))/(A(ΔABC))`
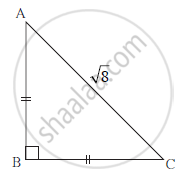
With the help of the information given in the figure, fill in the boxes to find AB and BC .
AB = BC (Given)
∴∠ BAC = ∠ BCA =
∴ AB = BC = × AC
= × `sqrt8`
= × `2sqrt2`
= 2
If ΔXYZ ~ ΔLMN, write the corresponding angles of the two triangles and also write the ratios of corresponding sides.
In Δ XYZ, XY = 4 cm, YZ = 6 cm, XZ = 5 cm, If ΔXYZ ~ ΔPQR and PQ = 8 cm then find the lengths of remaining sides of ΔPQR.
Draw a sketch of a pair of similar triangles. Label them. Show their corresponding angles by the same signs. Show the lengths of corresponding sides by numbers in proportion.
In the following figure, state whether the triangles are similar. Give reason.