Advertisements
Advertisements
Question
In the following figure, state whether the triangles are similar. Give reason.
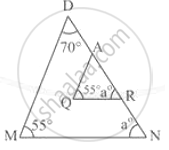
Solution
Yes, the triangles are similar because of the Angle-angel -angle similarity.
⇒ ∠M = ∠Q = (each angle is 55°)
⇒ ∠N = ∠R = (each angle is a°)
∴Due to AA similar, these two triangles are similar.
APPEARS IN
RELATED QUESTIONS
ΔDEF ~ ΔMNK. If DE = 5, MN = 6, then find the value of `"A(ΔDEF)"/"A(ΔMNK)"`
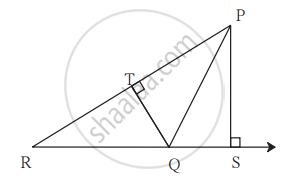
In adjoining figure, seg PS ⊥ seg RQ, seg QT ⊥ seg PR. If RQ = 6, PS = 6 and PR = 12, then Find QT.
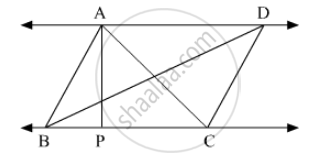
In the following figure, AP ⊥ BC, AD || BC, then find A(∆ABC) : A(∆BCD).
Select the correct alternative answer and write it.
The ratio of corresponding sides of similar triangles is 5 : 7, then what is
the ratio of their areas ?
(A)25 : 49 (B) 49 : 25 (C) 5 : 7 (D) 7 : 5
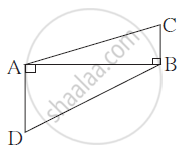
In the given figure, CB ⊥ AB, DA ⊥ AB.
if BC = 4, AD = 8 then `(A(Δ ABC))/(A(Δ ADB))` find.
Δ ABC ∼ Δ PQR. If A(Δ ABC)=25, A(ΔPQR)=16, find AB : PQ.
(A) 25:16
(B) 4:5
(C) 16:25
(D) 5:4
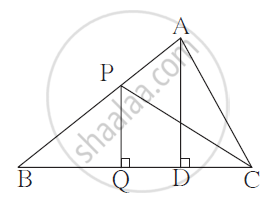
In the adjoining figure,
PQ ⊥ BC, AD ⊥ BC,
PQ = 4, AD = 6
Write down the following ratios.
(i)`(A(ΔPQB))/(A(ΔADB))`
(ii)`(A(ΔPBC))/(A(ΔABC))`
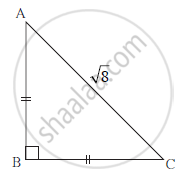
With the help of the information given in the figure, fill in the boxes to find AB and BC .
AB = BC (Given)
∴∠ BAC = ∠ BCA =
∴ AB = BC = × AC
= × `sqrt8`
= × `2sqrt2`
= 2
Prove that an equilateral triangle is equiangular.
If ΔXYZ ~ ΔLMN, write the corresponding angles of the two triangles and also write the ratios of corresponding sides.
In Δ XYZ, XY = 4 cm, YZ = 6 cm, XZ = 5 cm, If ΔXYZ ~ ΔPQR and PQ = 8 cm then find the lengths of remaining sides of ΔPQR.
Draw a sketch of a pair of similar triangles. Label them. Show their corresponding angles by the same signs. Show the lengths of corresponding sides by numbers in proportion.
