Advertisements
Advertisements
Question
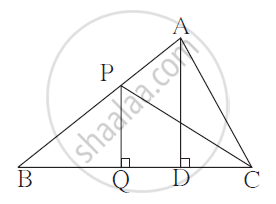
In the adjoining figure,
PQ ⊥ BC, AD ⊥ BC,
PQ = 4, AD = 6
Write down the following ratios.
(i)`(A(ΔPQB))/(A(ΔADB))`
(ii)`(A(ΔPBC))/(A(ΔABC))`
Solution
(i) In ΔPQB and ΔADB ,
∠B ≅ ∠B
∠PQB ≅ ∠ADB ................. (each right angle)
∴ ΔPQB ∼ ΔADB ................. (A-A test of similarty)
∴`(A(Delta PQB))/(A(DeltaABC)) = (PQ)^2/(AD)^2 = 4^2/6^2 = 16/36 = 4/9 `.......(Theorem of areas of similar triangle)
(ii) `(A(DeltaPBC))/(A(Delta ABC)) =(PQ)/(AD) = 4/6 = 2/3`.....(triangles having equal bases)
APPEARS IN
RELATED QUESTIONS
ΔDEF ~ ΔMNK. If DE = 5, MN = 6, then find the value of `"A(ΔDEF)"/"A(ΔMNK)"`
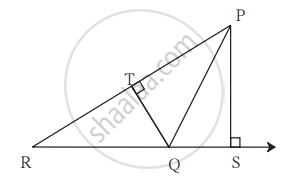
In adjoining figure, seg PS ⊥ seg RQ, seg QT ⊥ seg PR. If RQ = 6, PS = 6 and PR = 12, then Find QT.
In the following figure, AP ⊥ BC, AD || BC, then find A(∆ABC) : A(∆BCD).
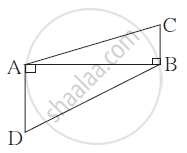
In the given figure, CB ⊥ AB, DA ⊥ AB.
if BC = 4, AD = 8 then `(A(Δ ABC))/(A(Δ ADB))` find.
Δ ABC ∼ Δ PQR. If A(Δ ABC)=25, A(ΔPQR)=16, find AB : PQ.
(A) 25:16
(B) 4:5
(C) 16:25
(D) 5:4
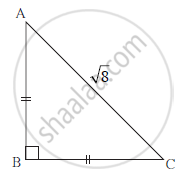
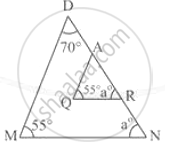
With the help of the information given in the figure, fill in the boxes to find AB and BC .
AB = BC (Given)
∴∠ BAC = ∠ BCA =
∴ AB = BC = × AC
= × `sqrt8`
= × `2sqrt2`
= 2
Prove that an equilateral triangle is equiangular.
If ΔXYZ ~ ΔLMN, write the corresponding angles of the two triangles and also write the ratios of corresponding sides.
In Δ XYZ, XY = 4 cm, YZ = 6 cm, XZ = 5 cm, If ΔXYZ ~ ΔPQR and PQ = 8 cm then find the lengths of remaining sides of ΔPQR.
Draw a sketch of a pair of similar triangles. Label them. Show their corresponding angles by the same signs. Show the lengths of corresponding sides by numbers in proportion.
In the following figure, state whether the triangles are similar. Give reason.