Advertisements
Advertisements
Question
In Quincke's experiment, the sound intensity has a minimum value l at a particular position. As the sliding tube is pulled out by a distance of 16.5 mm, the intensity increases to a maximum of 9 l. Take the speed of sound in air to be 330 m s−1. (a) Find the frequency of the sound source. (b) Find the ratio of the amplitudes of the two waves arriving at the detector assuming that it does not change much between the positions of minimum intensity and maximum intensity.
Solution
The sliding tube is pulled out by a distance of 16.5 mm.
Speed of sound in air, v = 330 ms−1
(a) As per the question, we have :
\[\frac{\lambda}{4} = 16 . 5 \text { mm }\]
\[ \Rightarrow \lambda = 16 . 5 \times 4 = 66 \text{ mm } = 66 \times {10}^{- 3} \text { m }\]
We know:
v = f\[\lambda\]
\[\therefore f = \frac{v}{\lambda}\]
\[\Rightarrow f = \frac{v}{\lambda} = \frac{340}{66 \times {10}^{- 3}} = 5 \text { kHz }\]
(b)
Ratio of maximum intensity to minimum intensity:
\[\frac{I_{Max}}{I_{Min}} = \frac{K \left( A_1 - A_2 \right)^2}{K \left( A_1 + A_2 \right)^2} = \frac{I}{9I}\]
\[ \Rightarrow \frac{\left( A_1 - A_2 \right)^2}{\left( A_1 + A_2 \right)^2} = \frac{1}{9}\]
\[\text { Taking square roots of both sides, we get: }\]
\[\frac{A_1 + A_2}{A_1 - A_2} = \frac{3}{1}\]
\[\Rightarrow\frac{A_1}{A_2}=\frac{3 + 1}{3 - 1}=\frac{2}{1}\]
So, the ratio of the amplitudes is 2.
APPEARS IN
RELATED QUESTIONS
Which of the following is a mechanical wave?
Two waves represented by \[y = a\sin\left( \omega t - kx \right)\] and \[y = a\cos\left( \omega t - kx \right)\] \[y = a\cos\left( \omega t - kx \right)\] are superposed. The resultant wave will have an amplitude
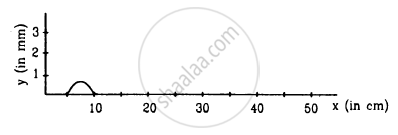
following Figure shows a wave pulse at t = 0. The pulse moves to the right with a speed of 10 cm s−1. Sketch the shape of the string at t = 1 s, 2 s and 3 s.
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
The speed of sound in a medium depends on
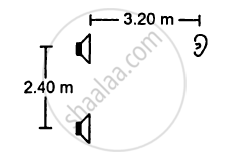
Two stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air = 320 m s−1.
Find the fundamental, first overtone and second overtone frequencies of an open organ pipe of length 20 cm. Speed of sound in air is 340 ms−1.
A cylindrical metal tube has a length of 50 cm and is open at both ends. Find the frequencies between 1000 Hz and 2000 Hz at which the air column in the tube can resonate. Speed of sound in air is 340 m s−1.
Find the greatest length of an organ pipe open at both ends that will have its fundamental frequency in the normal hearing range (20 − 20,000 Hz). Speed of sound in air = 340 m s−1.
An electronically driven loudspeaker is placed near the open end of a resonance column apparatus. The length of air column in the tube is 80 cm. The frequency of the loudspeaker can be varied between 20 Hz and 2 kHz. Find the frequencies at which the column will resonate. Speed of sound in air = 320 m s−1.
A piston is fitted in a cylindrical tube of small cross section with the other end of the tube open. The tube resonates with a tuning fork of frequency 512 Hz. The piston is gradually pulled out of the tube and it is found that a second resonance occurs when the piston is pulled out through a distance of 32.0 cm. Calculate the speed of sound in the air of the tube.
Calculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2 cm. The speed of sound in air is 350 m s−1.
A bat emitting an ultrasonic wave of frequency 4.5 × 104 Hz flies at a speed of 6 m s−1between two parallel walls. Find the fractional heard by the bat and the beat frequencies heard by the bat and the beat frequency between the two. The speed of sound is 330 m s−1.
A violin player riding on a slow train plays a 440 Hz note. Another violin player standing near the track plays the same note. When the two are closed by and the train approaches the person on the ground, he hears 4.0 beats per second. The speed of sound in air = 340 m s−1. (a) Calculate the speed of the train. (b) What beat frequency is heard by the player in the train?
A small source of sound vibrating at frequency 500 Hz is rotated in a circle of radius 100/π cm at a constant angular speed of 5.0 revolutions per second. A listener situation situates himself in the plane of the circle. Find the minimum and the maximum frequency of the sound observed. Speed of sound in air = 332 m s−1.
A source emitting sound at frequency 4000 Hz, is moving along the Y-axis with a speed of 22 m s−1. A listener is situated on the ground at the position (660 m, 0). Find the frequency of the sound received by the listener at the instant the source crosses the origin. Speed of sound in air = 330 m s−1.
A source emitting a sound of frequency v is placed at a large distance from an observer. The source starts moving towards the observer with a uniform acceleration a. Find the frequency heard by the observer corresponding to the wave emitted just after the source starts. The speed of sound in the medium is v.
A wave of frequency 500 Hz is traveling with a speed of 350 m/s. (a) What is the phase difference between two displacements at a certain point at times 1.0 ms apart? (b) what will be the smallest distance between two points which are 45° out of phase at an instant of time?
The speed of sound in hydrogen is 1270 m/s. The speed of sound in the mixture of oxygen and hydrogen in which they are mixed in 1:4 ratio is
