Advertisements
Advertisements
Question
A wave of frequency 500 Hz is traveling with a speed of 350 m/s. (a) What is the phase difference between two displacements at a certain point at times 1.0 ms apart? (b) what will be the smallest distance between two points which are 45° out of phase at an instant of time?
Solution
Given: n = 500 Hz, v = 350 m/s
v = n × λ
∴ λ = `350/500` = 0.7 m
(a) The path difference is the distance covered v × t = 350 × 0.001 = 0.35 m at t = 1.0 ms = 0.001 s.
∴ Phase difference = `(2π)/λxx"Path difference"`
= `(2π)/0.7xx0.35` = π rad
(b) Phase difference = 45° = `π/4` rad
∴ Path difference = `λ/(2π)xx"Phase difference"`
= `0.7/(2π)xxπ/4` = 0.0875 m
RELATED QUESTIONS
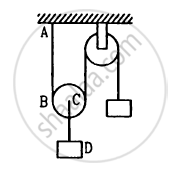
Both the strings, shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is
\[\nu_1\] and in CD it is \[\nu_2\]. Then \[\nu_1 / \nu_2\]
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
In a stationary wave,
(a) all the particles of the medium vibrate in phase
(b) all the antinodes vibrates in phase
(c) the alternate antinodes vibrate in phase
(d) all the particles between consecutive nodes vibrate in phase.
A wave is described by the equation \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right) .\]
(a) Find the time period and the wavelength? (b) Write the equation for the velocity of the particles. Find the speed of the particle at x = 1⋅0 cm at time t = 0⋅01 s. (c) What are the speeds of the particles at x = 3⋅0 cm, 5⋅0 cm and 7⋅0 cm at t = 0⋅01 s?
(d) What are the speeds of the particles at x = 1⋅0 cm at t = 0⋅011, 0⋅012, and 0⋅013 s?
A string of linear mass density 0⋅5 g cm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end (See figure). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20 cm s−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to region its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string?
The speed of sound in a medium depends on
In Quincke's experiment, the sound intensity has a minimum value l at a particular position. As the sliding tube is pulled out by a distance of 16.5 mm, the intensity increases to a maximum of 9 l. Take the speed of sound in air to be 330 m s−1. (a) Find the frequency of the sound source. (b) Find the ratio of the amplitudes of the two waves arriving at the detector assuming that it does not change much between the positions of minimum intensity and maximum intensity.
Two audio speakers are kept some distance apart and are driven by the same amplifier system. A person is sitting at a place 6.0 m from one of the speakers and 6.4 m from the other. If the sound signal is continuously varied from 500 Hz to 5000 Hz, what are the frequencies for which there is a destructive interference at the place of the listener? Speed of sound in air = 320 m s−1.
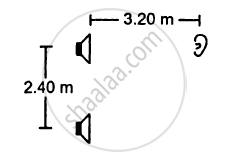
Two stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air = 320 m s−1.
A closed organ pipe can vibrate at a minimum frequency of 500 Hz. Find the length of the tube. Speed of sound in air = 340 m s−1.
A copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8 km s−1.
Find the greatest length of an organ pipe open at both ends that will have its fundamental frequency in the normal hearing range (20 − 20,000 Hz). Speed of sound in air = 340 m s−1.
An open organ pipe has a length of 5 cm. (a) Find the fundamental frequency of vibration of this pipe. (b) What is the highest harmonic of such a tube that is in the audible range? Speed of sound in air is 340 m s−1 and the audible range is 20-20,000 Hz.
An electronically driven loudspeaker is placed near the open end of a resonance column apparatus. The length of air column in the tube is 80 cm. The frequency of the loudspeaker can be varied between 20 Hz and 2 kHz. Find the frequencies at which the column will resonate. Speed of sound in air = 320 m s−1.
Two successive resonance frequencies in an open organ pipe are 1944 Hz and 2592 Hz. Find the length of the tube. The speed of sound in air is 324 ms−1.
A Kundt's tube apparatus has a copper rod of length 1.0 m clamped at 25 cm from one of the ends. The tube contains air in which the speed of sound is 340 m s−1. The powder collects in heaps separated by a distance of 5.0 cm. Find the speed of sound waves in copper.
A tuning fork of unknown frequency makes 5 beats per second with another tuning fork which can cause a closed organ pipe of length 40 cm to vibrate in its fundamental mode. The beat frequency decreases when the first tuning fork is slightly loaded with wax. Find its original frequency. The speed of sound in air is 320 m s−1.
The horn of a car emits sound with a dominant frequency of 2400 Hz. What will be the apparent dominant frequency heard by a person standing on the road in front of the car if the car is approaching at 18.0 km h−1? Speed of sound in air = 340 m s−1.
A train approaching a platform at a speed of 54 km h−1 sounds a whistle. An observer on the platform finds its frequency to be 1620 Hz. the train passes the platform keeping the whistle on and without slowing down. What frequency will the observer hear after the train has crossed the platform? The speed of sound in air = 332 m s−1.
A bullet passes past a person at a speed of 220 m s−1. Find the fractional change in the frequency of the whistling sound heard by the person as the bullet crosses the person. Speed of sound in air = 330 m s−1.
A violin player riding on a slow train plays a 440 Hz note. Another violin player standing near the track plays the same note. When the two are closed by and the train approaches the person on the ground, he hears 4.0 beats per second. The speed of sound in air = 340 m s−1. (a) Calculate the speed of the train. (b) What beat frequency is heard by the player in the train?
A car moving at 108 km h−1 finds another car in front it going in the same direction at 72 km h−1. The first car sounds a horn that has a dominant frequency of 800 Hz. What will be the apparent frequency heard by the driver in the front car? Speed of sound in air = 330 m s−1.
A source emitting a sound of frequency v is placed at a large distance from an observer. The source starts moving towards the observer with a uniform acceleration a. Find the frequency heard by the observer corresponding to the wave emitted just after the source starts. The speed of sound in the medium is v.
The speed of sound in hydrogen is 1270 m/s. The speed of sound in the mixture of oxygen and hydrogen in which they are mixed in 1:4 ratio is
The speed of a transverse wave in an elastic string is v0. If the tension in the string is reduced to half, then the speed of the wave is given by:
Change in temperature of the medium changes ______.
A spring breaks under tension of 10 kg wt.If the string is used to revolve a body of mass 1.2 kg in a horizontal circle. of radius 50 cm, what is the maximum speed with which a body can be revolved?
