Advertisements
Advertisements
Question
A train approaching a platform at a speed of 54 km h−1 sounds a whistle. An observer on the platform finds its frequency to be 1620 Hz. the train passes the platform keeping the whistle on and without slowing down. What frequency will the observer hear after the train has crossed the platform? The speed of sound in air = 332 m s−1.
Solution
Given:
Speed of sound in air v= 332 ms−1
Velocity of train \[v_s\] = 54 kmh−1 =\[54 \times \frac{5}{18} \text{ m/s } = 15 \text { m/s }\]
Let
\[f_0\] be the original frequency of the train.
When the train approaches a platform, the frequency of sound heard by the observer \[\left( f \right)\] is given by :
\[f = \left( \frac{v}{v - v_s} \right) \times f_0\]
On substituting the values, we have:
\[1620 = \left( \frac{332}{332 - 15} \right) f_0 \]
\[ \Rightarrow f_0 = \left( \frac{1620 \times 317}{332} \right) \text { Hz } .\]
When the train crosses the platform, the frequency of sound heard by the observer \[\left( f_1 \right)\] is given by :
\[f_1 = \left( \frac{v}{v + v_s} \right) \times f_0\]
Substituting the respective values in the above formula, we have:
\[f_1 = \left( \frac{332}{332 + 15} \times \frac{1620 \times 317}{332} \right)\]
\[ = \frac{317}{347} \times 1620 = 1480 \text { Hz }\]
APPEARS IN
RELATED QUESTIONS
Two periodic waves of amplitudes A1 and A2 pass thorough a region. If A1 > A2, the difference in the maximum and minimum resultant amplitude possible is
The fundamental frequency of a string is proportional to
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
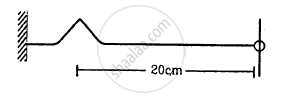
A string of linear mass density 0⋅5 g cm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end (See figure). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20 cm s−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to region its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string?
At a prayer meeting, the disciples sing JAI-RAM JAI-RAM. The sound amplified by a loudspeaker comes back after reflection from a building at a distance of 80 m from the meeting. What maximum time interval can be kept between one JAI-RAM and the next JAI-RAM so that the echo does not disturb a listener sitting in the meeting. Speed of sound in air is 320 m s−1.
Calculate the speed of sound in oxygen from the following data. The mass of 22.4 litre of oxygen at STP (T = 273 K and p = 1.0 × 105 N m−2) is 32 g, the molar heat capacity of oxygen at constant volume is Cv = 2.5 R and that at constant pressure is Cp = 3.5 R.
A one-metre long stretched string having a mass of 40 g is attached to a tuning fork. The fork vibrates at 128 Hz in a direction perpendicular to the string. What should be the tension in the string if it is to vibrate in four loops?
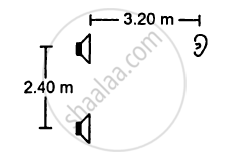
Two stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air = 320 m s−1.
A cylindrical metal tube has a length of 50 cm and is open at both ends. Find the frequencies between 1000 Hz and 2000 Hz at which the air column in the tube can resonate. Speed of sound in air is 340 m s−1.
Find the greatest length of an organ pipe open at both ends that will have its fundamental frequency in the normal hearing range (20 − 20,000 Hz). Speed of sound in air = 340 m s−1.
An open organ pipe has a length of 5 cm. (a) Find the fundamental frequency of vibration of this pipe. (b) What is the highest harmonic of such a tube that is in the audible range? Speed of sound in air is 340 m s−1 and the audible range is 20-20,000 Hz.
Two successive resonance frequencies in an open organ pipe are 1944 Hz and 2592 Hz. Find the length of the tube. The speed of sound in air is 324 ms−1.
A U-tube having unequal arm-lengths has water in it. A tuning fork of frequency 440 Hz can set up the air in the shorter arm in its fundamental mode of vibration and the same tuning fork can set up the air in the longer arm in its first overtone vibration. Find the length of the air columns. Neglect any end effect and assume that the speed of sound in air = 330 m s−1.
A Kundt's tube apparatus has a copper rod of length 1.0 m clamped at 25 cm from one of the ends. The tube contains air in which the speed of sound is 340 m s−1. The powder collects in heaps separated by a distance of 5.0 cm. Find the speed of sound waves in copper.
The horn of a car emits sound with a dominant frequency of 2400 Hz. What will be the apparent dominant frequency heard by a person standing on the road in front of the car if the car is approaching at 18.0 km h−1? Speed of sound in air = 340 m s−1.
A bat emitting an ultrasonic wave of frequency 4.5 × 104 Hz flies at a speed of 6 m s−1between two parallel walls. Find the fractional heard by the bat and the beat frequencies heard by the bat and the beat frequency between the two. The speed of sound is 330 m s−1.
A violin player riding on a slow train plays a 440 Hz note. Another violin player standing near the track plays the same note. When the two are closed by and the train approaches the person on the ground, he hears 4.0 beats per second. The speed of sound in air = 340 m s−1. (a) Calculate the speed of the train. (b) What beat frequency is heard by the player in the train?
A small source of sound vibrating at frequency 500 Hz is rotated in a circle of radius 100/π cm at a constant angular speed of 5.0 revolutions per second. A listener situation situates himself in the plane of the circle. Find the minimum and the maximum frequency of the sound observed. Speed of sound in air = 332 m s−1.
An operator sitting in his base camp sends a sound signal of frequency 400 Hz. The signal is reflected back from a car moving towards him. The frequency of the reflected sound is found to be 410 Hz. Find the speed of the car. Speed of sound in air = 324 m s−1
A spring breaks under tension of 10 kg wt.If the string is used to revolve a body of mass 1.2 kg in a horizontal circle. of radius 50 cm, what is the maximum speed with which a body can be revolved?
