Advertisements
Advertisements
Question
An open organ pipe has a length of 5 cm. (a) Find the fundamental frequency of vibration of this pipe. (b) What is the highest harmonic of such a tube that is in the audible range? Speed of sound in air is 340 m s−1 and the audible range is 20-20,000 Hz.
Solution
Given:
Length of organ pipe \[L\]= 5 cm = 5 × 10−2 m
v = 340 m/s
The audible range is from 20 Hz to 20,000 Hz.
The fundamental frequency of an open organ pipe is : \[f = \frac{v}{2L}\]
On substituting the respective values ,we get : \[f = \frac{340}{2 \times 2 \times {10}^{- 2}} = 3 . 4 \text { kHz }\]
(b) If the fundamental frequency is 3.4 kHz, then the highest harmonic in the audible range (20 Hz - 20 kHz) is
Required highest harmonic =\[\frac{20, 000}{3400} = 5 . 8 = 5\]
APPEARS IN
RELATED QUESTIONS
Which of the following is a mechanical wave?
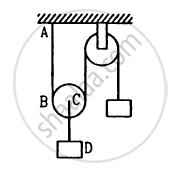
Both the strings, shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is
\[\nu_1\] and in CD it is \[\nu_2\]. Then \[\nu_1 / \nu_2\]
Two periodic waves of amplitudes A1 and A2 pass thorough a region. If A1 > A2, the difference in the maximum and minimum resultant amplitude possible is
Two particles A and B have a phase difference of π when a sine wave passes through the region.
(a) A oscillates at half the frequency of B.
(b) A and B move in opposite directions.
(c) A and B must be separated by half of the wavelength.
(d) The displacements at A and B have equal magnitudes.
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
A wave is described by the equation \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right) .\]
(a) Find the time period and the wavelength? (b) Write the equation for the velocity of the particles. Find the speed of the particle at x = 1⋅0 cm at time t = 0⋅01 s. (c) What are the speeds of the particles at x = 3⋅0 cm, 5⋅0 cm and 7⋅0 cm at t = 0⋅01 s?
(d) What are the speeds of the particles at x = 1⋅0 cm at t = 0⋅011, 0⋅012, and 0⋅013 s?
Find the change in the volume of 1.0 litre kerosene when it is subjected to an extra pressure of 2.0 × 105 N m−2 from the following data. Density of kerosene = 800 kg m−3and speed of sound in kerosene = 1330 ms−1.
In Quincke's experiment, the sound intensity has a minimum value l at a particular position. As the sliding tube is pulled out by a distance of 16.5 mm, the intensity increases to a maximum of 9 l. Take the speed of sound in air to be 330 m s−1. (a) Find the frequency of the sound source. (b) Find the ratio of the amplitudes of the two waves arriving at the detector assuming that it does not change much between the positions of minimum intensity and maximum intensity.
Two audio speakers are kept some distance apart and are driven by the same amplifier system. A person is sitting at a place 6.0 m from one of the speakers and 6.4 m from the other. If the sound signal is continuously varied from 500 Hz to 5000 Hz, what are the frequencies for which there is a destructive interference at the place of the listener? Speed of sound in air = 320 m s−1.
A copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8 km s−1.
A piston is fitted in a cylindrical tube of small cross section with the other end of the tube open. The tube resonates with a tuning fork of frequency 512 Hz. The piston is gradually pulled out of the tube and it is found that a second resonance occurs when the piston is pulled out through a distance of 32.0 cm. Calculate the speed of sound in the air of the tube.
Calculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2 cm. The speed of sound in air is 350 m s−1.
The horn of a car emits sound with a dominant frequency of 2400 Hz. What will be the apparent dominant frequency heard by a person standing on the road in front of the car if the car is approaching at 18.0 km h−1? Speed of sound in air = 340 m s−1.
A bullet passes past a person at a speed of 220 m s−1. Find the fractional change in the frequency of the whistling sound heard by the person as the bullet crosses the person. Speed of sound in air = 330 m s−1.
Figure shows a person standing somewhere in between two identical tuning forks. each vibrating at 512 Hz. If both the tuning forks move towards right a speed of 5.5 m s−1, find the number of beats heard by the listener. Speed of sound in air = 330 m s−1.

Two trains are travelling towards each other both at a speed of 90 km h−1. If one of the trains sounds a whistle at 500 Hz, what will be the apparent frequency heard in the other train? Speed of sound in air = 350 m s−1.
The speed of sound in hydrogen is 1270 m/s. The speed of sound in the mixture of oxygen and hydrogen in which they are mixed in 1:4 ratio is
A metallic wire of 1 m length has a mass of 10 × 10−3 kg. If the tension of 100 N is applied to a wire, what is the speed of the transverse wave?
