Advertisements
Advertisements
Question
In the figure, seg AB is a diameter of a circle with centre O. The bisector of ∠ACB intersects the circle at point D. Prove that, seg AD ≅ seg BD. Complete the following proof by filling in the blanks.
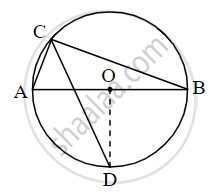
Proof:
Draw seg OD.
∠ACB = `square` ......[Angle inscribed in semicircle]
∠DCB = `square` ......[CD is the bisector of ∠C]
m(arc DB) = `square` ......[Inscribed angle theorem]
∠DOB = `square` ......[Definition of measure of an arc](i)
seg OA ≅ seg OB ...... `square` (ii)
∴ Line OD is `square` of seg AB ......[From (i) and (ii)]
∴ seg AD ≅ seg BD
Solution
Proof:
∠ACB = 90° ......[Angle inscribed in semicircle]
∠DCB = ∠DCA = 45° ......[CD is the bisector of ∠C]
m(arc DB) = 2∠DCB = 90° ......[Inscribed angle theorem]
∠DOB = m(arc DB) = 90° ......[Definition of measure of an arc](i)
seg OA ≅ seg OB ......[Radii of the same circle] (ii)
∴ Line OD is perpendicular bisector of seg AB ......[From (i) and (ii)]
∴ seg AD ≅ seg BD
APPEARS IN
RELATED QUESTIONS
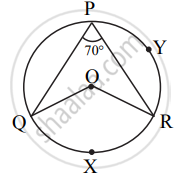
In the given figure, O is the centre of the circle, ∠QPR = 70° and m(arc PYR) = 160°, then find the value of the following m(arc QXR).
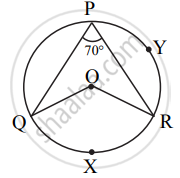
In the given figure, O is centre of circle. ∠QPR = 70° and m(arc PYR) = 160°, then find the value of the following ∠QOR.
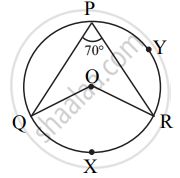
In the given figure, O is centre of circle, ∠QPR = 70° and m(arc PYR) = 160°, then find the value of the following ∠PQR.

A circle with centre P is inscribed in the ABC. Side AB, side BC and side AC touch the circle at points L, M and N respectively. Radius of the circle is r.
Prove that: `"A" (triangle "ABC") =1/2 ("AB" + "BC" + "AC") xx "r"`
In the figure, if the chord PQ and chord RS intersect at point T, prove that: m∠STQ = `1/2` [m(arc PR) + m(arc SQ)] for any measure of ∠STQ by filling out the boxes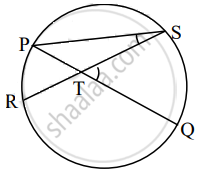
Proof: m∠STQ = m∠SPQ + `square` .....[Theorem of the external angle of a triangle]
= `1/2` m(arc SQ) + `square` .....[Inscribed angle theorem]
= `1/2 [square + square]`
In figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.
Proof: Draw seg GF.
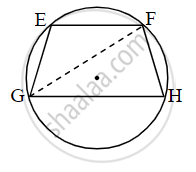
∠EFG = ∠FGH ......`square` .....(I)
∠EFG = `square` ......[inscribed angle theorem] (II)
∠FGH = `square` ......[inscribed angle theorem] (III)
∴ m(arc EG) = `square` ......[By (I), (II), and (III)]
chord EG ≅ chord FH ........[corresponding chords of congruent arcs]
The angle inscribed in the semicircle is a right angle. Prove the result by completing the following activity.

Given: ∠ABC is inscribed angle in a semicircle with center M
To prove: ∠ABC is a right angle.
Proof: Segment AC is a diameter of the circle.
∴ m(arc AXC) = `square`
Arc AXC is intercepted by the inscribed angle ∠ABC
∠ABC = `square` ......[Inscribed angle theorem]
= `1/2 xx square`
∴ m∠ABC = `square`
∴ ∠ABC is a right angle.
In the figure, a circle with center C has m(arc AXB) = 100° then find central ∠ACB and measure m(arc AYB).
In the figure, chord LM ≅ chord LN, ∠L = 35°.

Find
(i) m(arc MN)
(ii) m(arc LN)
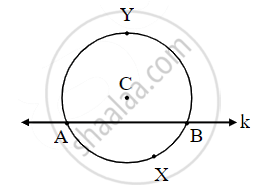
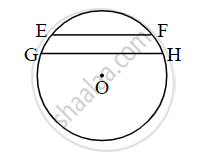
In the figure, if O is the center of the circle and two chords of the circle EF and GH are parallel to each other. Show that ∠EOG ≅ ∠FOH
In the figure, ΔABC is an equilateral triangle. The angle bisector of ∠B will intersect the circumcircle ΔABC at point P. Then prove that: CQ = CA.

In the above figure, chord PQ and chord RS intersect each other at point T. If ∠STQ = 58° and ∠PSR = 24°, then complete the following activity to verify:

∠STQ = `1/2` [m(arc PR) + m(arc SQ)]
Activity: In ΔPTS,
∠SPQ = ∠STQ – `square` ......[∵ Exterior angle theorem]
∴ ∠SPQ = 34°
∴ m(arc QS) = 2 × `square`° = 68° ....... ∵ `square`
Similarly, m(arc PR) = 2∠PSR = `square`°
∴ `1/2` [m(arc QS) + m(arc PR)] = `1/2` × `square`° = 58° ......(I)
But ∠STQ = 58° .....(II) (given)
∴ `1/2` [m(arc PR) + m(arc QS)] = ∠______ ......[From (I) and (II)]
In the figure, the centre of the circle is O and ∠STP = 40°.
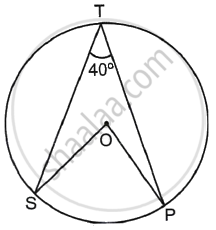
- m (arc SP) = ? By which theorem?
- m ∠SOP = ? Give reason.
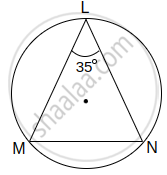
In the above figure, ∠L = 35°, find :
- m(arc MN)
- m(arc MLN)
Solution :
- ∠L = `1/2` m(arc MN) ............(By inscribed angle theorem)
∴ `square = 1/2` m(arc MN)
∴ 2 × 35 = m(arc MN)
∴ m(arc MN) = `square` - m(arc MLN) = `square` – m(arc MN) ...........[Definition of measure of arc]
= 360° – 70°
∴ m(arc MLN) = `square`
