Advertisements
Advertisements
Question
In the following figure, triangle ABC is equilateral and triangle PBC is isosceles. If PBA = 20°; find angle BPC.
Solution
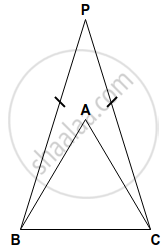
In the above figure,
∠PBA = ∠ABC + ∠PBA = 60° + 20° = 80°
But ΔPBC is an isosceles triangle
∴ ∠PCB = ∠PBC = 80°
But ∠PBC + ∠PCB + ∠BPC = 180° ...(Sum of angles of a triangle)
⇒ 80° + 80° + ∠BPC = 180°
⇒ 160° + ∠BPC = 180°
∠BPC = 180° - 160° = 20°
APPEARS IN
RELATED QUESTIONS
Construct traingle ABC, when: BC = 3 cm, AC = 4 cm and AB = 5 cm. Measure angle ACB. Give a special name to this triangle.
If each of the two equal angles of an isosceles triangle is 68°, find the third angle.
The angles of a triangle are in the ratio 3:5: 7. Find each angle.
In the following figure, triangle ABC is equilateral and triangle PBC is isosceles. If PBA = 20°; find angle PBC.
Construct a triangle ABC given AB = 6 cm, BC = 5 cm and CA = 5.6 cm. From vertex A draw a perpendicular on to side BC. Measure the length of this perpendicular.
Observe the figure below and write the type of the triangle based on its sides.
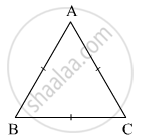
Δ ABC is ... triangle
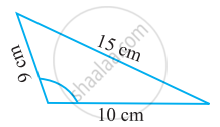
Name the following triangle in two different ways: (you may judge the nature of the angle by observation)
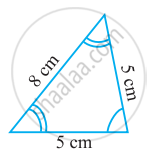
Name the following triangle in two different ways: (you may judge the nature of the angle by observation)
Name polygon.

Make two more examples of this.
A diagonal is a line segment that joins any two vertices of the polygon and is not a side of the polygon. Draw a rough sketch of a pentagon and draw its diagonals.
