Advertisements
Advertisements
Question
In the given figure,
(1) m(arc CE) = 54°, m(arc BD) = 23°, find measure of ∠CAE.
(2) If AB = 4.2, BC = 5.4, AE = 12.0, find AD.
(3) If AB = 3.6, AC = 9.0, AD = 5.4, find AE.
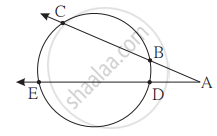
Solution
(1) m(arc CE) = 54°, m(arc BD) = 23°
∠CAE has its vertex outside the circle and intercept and CE and BD.
If two lines containing chords of a circle intersect each other outside the circle, then the measure of angle between them is half the difference in measures of the arcs intercepted by the angle.
∴ ∠CAE = `1/2` × [m(arc CE) - m(arc BD)]
∴ ∠CAE = `1/2` × [54 - 23]
∴ ∠CAE = `1/2` × 31
∴ ∠CAE = 15.5º
(2) AB = 4.2, BC = 5.4, AE = 12 ...(Given)
AC = AB + BC ...(A - B - C)
∴ AC = 4.2 + 5.4
∴ AC = 9.6
Chord CB and chord ED intersect at point A outside the circle.
∴ by theorem of external division of chords.
AB × AC = AD × AE
∴ 4.2 × 9.6 = AD × 12
∴ AD = `(4.2×9.6)/12`
∴ AD = `(4.2 × 9.6 × 100)/(12 × 100)`
∴ AD = `(42 × 96)/(1200)`
∴ AD = `(42 × 8)/(100)`
∴ AD = 3.36
(3) AB = 3.6, AC = 9 cm and AD = 5.4 ...(Given )
chords CB and ED intersect at point A outside the circle.
∴ by theorem of external division of chords,
AB × AC = AD × AE
∴ 3.6 × 9 = 5.4 × AE
∴ AE = `(3.6 × 9)/5.4`
∴ AE = `(3.6 × 9 × 10)/(5.4 × 10)`
∴ AE = `(36 × 9)/54`
∴ AE = 6

