Advertisements
Advertisements
Question
In the given figure, AB = AC.
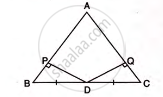
Prove that:
(i) DP = DQ
(ii) AP = AQ
(iii) AD bisects angle A
Sum
Solution
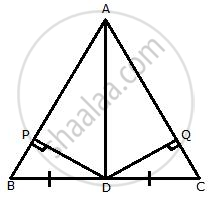
Const: Join AD.
In ΔABC,
AB = AC .......[Given]
∴ ∠C = ∠B ......(i) [angles opp. to equal sides are equal]
(i)
In ΔBPD and ΔCQD,
∠BPD = ∠CQD ......[Each = 90°]
∠B = ∠C ........[proved]
BD = DC ........[Given]
∴ ΔBPD ≅ ΔCQD .......[AAS criterion]
∴ DP = DQ ......[c.p.c.t]
(ii)
We have already proved that ΔBPD ≅ ΔCQD
Therefore, BP = CQ .......[c.p.c.t]
Now,
AB = AC .......[Given]
⇒ AB − BP = AC − CQ
⇒ AP = AQ
(iii)
In ΔAPD and ΔAQD,
DP = DQ .......[proved]
AD = AD .......[common]
AP = AQ ........[Proved]
∴ ΔAPD ≅ ΔAQD ......[SSS]
⇒ ∠PAD = ∠QAD .......[c.p.c.t]
Hence, AD bisects angle A.
shaalaa.com
Is there an error in this question or solution?
