Advertisements
Advertisements
Question
In the given figure, D and E are points on AB and AC respectively. AE and CD intersect at P such that AP = CP. If ∠BAE = ∠BCD, prove that DBDE is isosceles.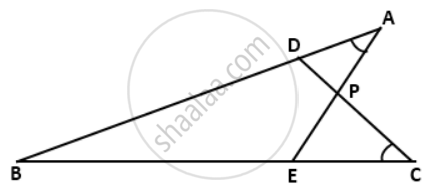
Solution
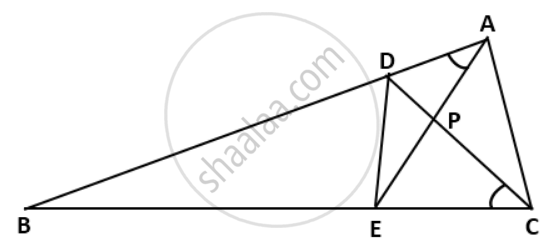
Join DE and AC
In ΔAPD = ΔEPC,
∠DAP = ∠ECP ....(∵ ∠BAE = ∠BCD)
AP = CP ....(given)
∠APD = ∠EPC ....(vertically opposite angles)
∴ ΔAPD ≅ ΔEPC ....(By ASA Congruence critetion)
⇒ AD = EC ....(c.p.c.t)
In ΔAPC,
AP = CP ....(given)
⇒ ∠PAC = ∠PCA ....(angles opposite to two equal sides are equal)
Now, ∠BAC = ∠BCD and ∠PAC = ∠PCA
⇒ ∠BAC =∠BCA
⇒ BC = BA ....(sides opposites to two equal sides are equal)
⇒ BE + EC = BD + DA
⇒ BE = BD ....(∵ EC = DA)
⇒ ∠BDE = ∠BED ....(angles opposite to two equal sides are equal)
⇒ ΔBDE is an isosceles triangle.
