Advertisements
Advertisements
Question
ΔPQR is an isosceles triangle with PQ = PR. QR is extended to S and ST is drawn perpendicular to QP produced, and SN is perpendicular to PR produced. Prove that QS bisects ∠TSN.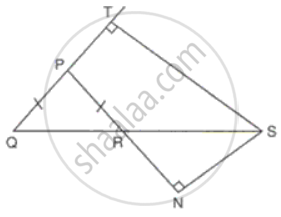
Solution
In ΔPQR, let ∠PQR = x
PQ = PR
⇒ ∠PQR = ∠PRQ = x ........(i)
In ΔRNS,
∠NRS = ∠PRQ = x .........(vertically opposite angles)
∠RNS = 90° ...(given)
∠NSR + ∠RNS + ∠NRS = 180°
∠NSR + 90° + x = 180
∠NSR = 90° - x .........(ii)
Now in Quadrilateral PTRS
∠PTS = 90° ...(given)
∠TPR = ∠PQR + ∠PRQ = 2x ....(exterior angle to triangle PQR)
∠PRS = 180° - ∠PRQ = 180° - x ...(QRS is a st. Line)
∠PTS + ∠TRP + ∠PRS + ∠TSR = 360° ...(angles of a quad. = 360°)
90° + 2x + 180° - x + ∠TSR = 360°
∠TSR = 90° - x ..........(iii)
From (ii) and (iii)
∠TSR = ∠NSR
Therefore, QS bisects ∠TSN.
