Advertisements
Advertisements
Question
In ΔXYZ, AY and AZ are the bisector of ∠Y and ∠Z respectively. The perpendicular bisectors of AY and AZ cut YZ at B and C respectively. Prove that line segment YZ is equal to the perimeter of ΔABC.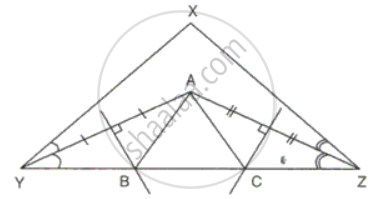
Sum
Solution
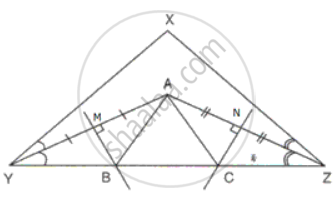
Let M and N be the points where AY and AZ are bisected.
In ΔABM and ΔBMY
MY = MA ...(BM bisects AY)
BM = BM ...(common)
∠BMY = ∠BMA
Therefore, ΔABM ≅ ΔBMY
Hence, YB = AB ..........(i)
In ΔACN and ΔCNZ
NZ = NA ...(CN bisects AZ)
CN = CN ...(common)
∠CAN = ∠CNZ
Therefore, ΔACN ≅ ΔCNZ
Hence, CZ = AC ............(ii)
YZ = YB + BC + CZ
Substituting from (i) and (ii)
YZ = AB + BC + AC
Hence, YZ is equal to the perimeter of ΔABC.
shaalaa.com
Is there an error in this question or solution?
