Advertisements
Advertisements
Question
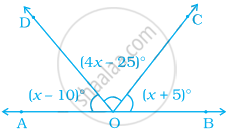
In the given figure, find the value of ∠BOC, if points A, O and B are collinear.
Solution
Since, A, O and B are collinear. Then, AOB will be a straight line and sum of all the angles on a straight line is 180°.
∴ ∠AOD + ∠DOC + ∠COB = 180°
⇒ (x – 10)° + (4x – 25)° + (x + 5)° = 180°
⇒ x – 10° + 4x – 25° + x + 5 = 180
⇒ 6x – 30° = 180°
⇒ 6x = 180° + 30°
⇒ 6x = 210°
⇒ x = 35°
Now, ∠BOC = (x + 5)°
= (35 + 5)°
= 40°
APPEARS IN
RELATED QUESTIONS
State, whether the following pair of line or ray appear to be parallel or intersecting.
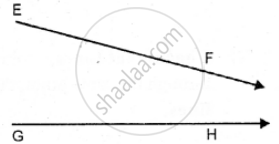
Under what condition will two straight lines, in the same plane, have only one point in common.
If possible draw a diagram in support of your answer.
The adjoining diagram shows a line AB. Draw diagram to represent: ray AB i.e. \[\underrightarrow{AB}\]

The adjoining diagram shows a ray AB. Draw diagrams to show the ray BA i.e. \[\underrightarrow{BA}\]
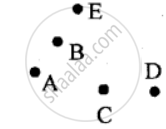
Use a ruler and whether following points are collinear or not:
A, B and E
State true or false; if false, give the correct statement:
Two parallel lines always lie in the same plane.
State true or false; if false, give the correct statement:
There are an infinite number of points in a line segment of length 10 cm.
Draw a figure to show that: lines AB, CD and EF are concurrent.
In figure is given below, write the number of line segments used:

Use the figure to name the A line.