Advertisements
Advertisements
Question
In the given figure, P is the point of contact.
(1) If m(arc PR) = 140°, ∠ POR = 36°, find m(arc PQ)
(2) If OP = 7.2, OQ = 3.2, find OR and QR
(3) If OP = 7.2, OR = 16.2, find QR.

Solution
Join PQ.

(1)
The measure of an inscribed angle is half of the measure of the arc intercepted by it.
∴ ∠PQR =\[\frac{1}{2}\] m(arc PR) = \[\frac{1}{2} \times 140°\] = 70º
In ∆POQ,
∠PQR = ∠POQ + ∠OPQ (Measure of an exterior angle of a triangle is equal to the sum of its remote interior angles)
⇒ 70º = 36º + ∠OPQ
⇒ ∠OPQ = 70º − 36º = 34º
The angle between a tangent of a circle and a chord drawn from the point of contact is congruent to the angle inscribed in the arc opposite to the arc intercepted by that angle.
∴ ∠PRQ = ∠OPQ = 34º
Now,
∠PRQ = \[\frac{1}{2}\]m(arc PQ) (The measure of an inscribed angle is half of the measure of the arc intercepted by it)
⇒ m(arc PQ) = 2∠PRQ = 2 × 34º = 68º
(2)
OP is the tangent and OQR is the secant.
∴ OQ × OR = OP2 (Tangent secant segment theorem)
⇒ 3.2 × OR = (7.2)2
⇒ OR = \[\frac{7 . 2 \times 7 . 2}{3 . 2}\] = 16.2 units
∴ QR = OR − OQ = 16.2 − 3.2 = 13 units
(3)
OP is the tangent and OQR is the secant.
∴ OQ × OR = OP2 (Tangent secant segment theorem)
⇒ OQ × 16.2 = (7.2)2
⇒ OQ = \[\frac{7 . 2 \times 7 . 2}{16 . 2}\] = 3.2 units
∴ QR = OR − OQ = 16.2 − 3.2 = 13 units
APPEARS IN
RELATED QUESTIONS
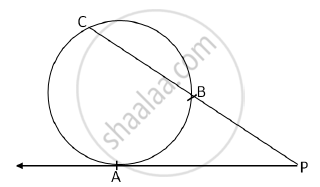
In the following figure, a tangent segment PA touching a circle in A and a secant PBC is shown. If AP = 15, BP = 10, find BC.
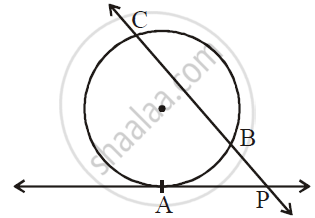
In the following figure, ray PA is a tangent to the circle at A and PBC is a secant. If AP = 15, BP = 10, then find BC.
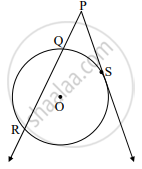
In the figure given above, ‘O’ is the centre of the circle, seg PS is a tangent segment and S is the point of contact. Line PR is a secant.
If PQ = 3.6, QR = 6.4, find PS.
Solution:
PS2 = PQ × `square` ......(tangent secant segments theorem)
= PQ × (PQ + `square`)
= 3.6 × (3.6 + 6.4)
= 3.6 × `square`
= 36
∴ PS = `square` .....(by taking square roots)
