Advertisements
Advertisements
Question
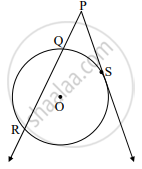
In the figure given above, ‘O’ is the centre of the circle, seg PS is a tangent segment and S is the point of contact. Line PR is a secant.
If PQ = 3.6, QR = 6.4, find PS.
Solution:
PS2 = PQ × `square` ......(tangent secant segments theorem)
= PQ × (PQ + `square`)
= 3.6 × (3.6 + 6.4)
= 3.6 × `square`
= 36
∴ PS = `square` .....(by taking square roots)
Solution
PS2 = PQ × PR ......(tangent secant segments theorem)
= PQ × (PQ + QR)
= 3.6 × (3.6 + 6.4)
= 3.6 × 10
= 36
∴ PS = 6 .....(by taking square roots)
APPEARS IN
RELATED QUESTIONS
In the following figure, a tangent segment PA touching a circle in A and a secant PBC is shown. If AP = 15, BP = 10, find BC.
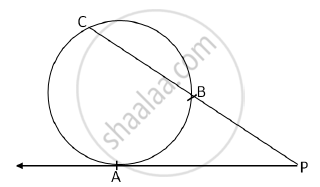
In the following figure, ray PA is a tangent to the circle at A and PBC is a secant. If AP = 15, BP = 10, then find BC.
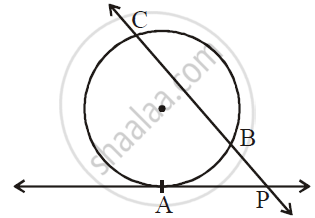
In the given figure, P is the point of contact.
(1) If m(arc PR) = 140°, ∠ POR = 36°, find m(arc PQ)
(2) If OP = 7.2, OQ = 3.2, find OR and QR
(3) If OP = 7.2, OR = 16.2, find QR.

