Question

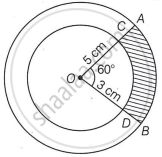
In the given figure, two concentric circles of radii 5 cm and 3 cm have their centre O. OAB is a sector of outer circle making an angle of 60° at the centre, while OCD is the sector of smaller circle. The area of the shaded region is ______.

Options

• `(7pi)/2  cm^2`

• `(8pi)/3  cm^2`

• `(25pi)/6  cm^2`

• `(3pi)/2  cm^2`

Answer 1

In the given figure, two concentric circles of radii 5 cm and 3 cm have their centre O. OAB is a sector of outer circle making an angle of 60° at the centre, while OCD is the sector of smaller circle. The area of the shaded region is `bbunderline((8pi)/3  cm^2)`.

Given, θ = 60°

OA = R = 5 cm and OD = r = 3 cm

∴ Area of shaded region= Area of sector OAB − Area of sector OCD

= `θ/(360°) xx πR^2 - θ/(360°) xx πr^2`

= `θ/(360°)  π(R^2 - r^2)`

= `(60°)/(360°)  π(5^2 - 3^2)`

= `8/3π`

Hence, the area of the shaded region is `8/3π  cm^2`.