English Medium
Academic Year: 2023-2024
Date & Time: 11th March 2024, 10:30 am
Duration: 3h
Advertisements
General Instructions:
- This question paper has 5 Sections A, B, C, D and E.
- Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
- Section B has 5 Short Answer-I (SA-I) type questions carrying 2 marks each.
- Section C has 6 Short Answer-II (SA-Il) type questions carrying 3 marks each.
- Section D has 4 Long Answer (LA) type questions carrying 5 marks each.
- Section E has 3 Case Based integrated units of assessment (4 marks each) with sub-parts of the values of 1, 1 and 2 marks each respectively.
- All questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Qs of 5 marks has been provided. An internal choice has been provided in the 2 marks question of Section E.
- Draw neat figures wherever required. Take `pi = 22/7` wherever required if not stated.
From an external point P, a tangent PA is drawn to circle. The number of tangents through P parallel to PA is ______.
2
more than 2
1
0
Chapter:
If the volume of a sphere is `11/21 "cm"^3`, then the radius of the sphere is ______.
2 cm
4 cm
`1/2` cm
`1/4` cm
Chapter:
In the given figure, graph of a polynomial f(x) is shown. The number of zeroes of polynomial f(x) is ______.
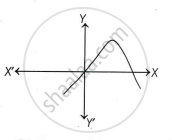
3
1
0
2
Chapter:
lf for a distribution `sum_1^n f_i x_i = 132 + 5p, sum_1^n f_i = 20` and mean of the distribution is 8.1, then the value of p is ______.
3
6
4
5
Chapter:
If in an AP, a = 2 and S10 = 335, then its 10th term is ______.
55
65
68
58
Chapter:
From a solid cube of side 14 cm, a sphere of maximum diameter is carved out. The radius of sphere is ______.
7 cm
14 cm
`7/2` cm
`sqrt(14)` cm
Chapter:
If the two zeroes of a quadratic polynomial are `± sqrt5` then the quadratic polynomial is ______.
x2 + 5
`(x + sqrt5)^2`
4(x2 - 5)
`x^2 - sqrt5`
Chapter:
In the given figure, tangents PA and PB drawn from P to circle are inclined to each other at an angle of 80°. The measure of ∠PAB is ______.
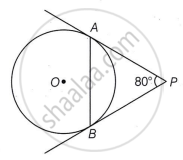
80°
60°
50°
40°
Chapter:
If in the given figure, DE || BC.
If AD = 2.8 cm, DB = 21 cm and EC = 4.8 cm, then the value of x is ______.
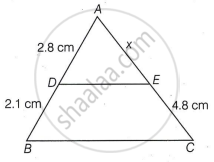
3.6 cm
2.4 cm
6.4 cm
4.8 cm
Chapter:
In a right angled ΔABC, ∠A = 90° and AB = AC. The value of sin C is ______.
0
`sqrt3/2`
`1/2`
`1/sqrt2`
Chapter:
Two fair coins are tossed together. The probability of getting 2 heads is ______.
`1/2`
`3/4`
`1/4`
`3/8`
Chapter:
If the mean and median of a data are 10 and 11 respectively, then mode of the data is ______.
12
8
20
13
Chapter:
If the distances of the points P(x , y) from (1, 0) and (0, 1) are equal, then which of the following is ______.
x + y = 0
x = y + 1
y = x + 1
x = y
Chapter:
The value(s) of k for which the quadratic equation 5x2 − 9kx + 5 = 0 has real and equal roots is/are ______.
`-10/9`
`±9/10`
`10/9`
`±10/9`
Chapter:
The lines represented by linear equations x = a and y = b (a ≠ b) are ______.
Intersecting at (a, b)
Intersecting at (b, a)
Parallel
Coincident
Chapter:
If cos θ = `1/sqrt2`, then tan θ is equal to ______.
`1/sqrt2`
0
1
`sqrt2 + 1`
Chapter:
A die is thrown once. The probability of getting a number less than 6 is ______.
0
`5/6`
`1/6`
1
Chapter:
Advertisements
In the given figure, two concentric circles of radii 5 cm and 3 cm have their centre O. OAB is a sector of outer circle making an angle of 60° at the centre, while OCD is the sector of smaller circle. The area of the shaded region is ______.
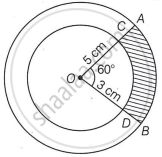
`(7pi)/2 cm^2`
`(8pi)/3 cm^2`
`(25pi)/6 cm^2`
`(3pi)/2 cm^2`
Chapter:
Assertion (A): The distance of P (a, b) from origin is a2 + b2.
Reason (R): The distance between two points `A(x_1, y_1) and B(x_2, y_2)` is `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`.
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
Assertion (A) is true but Reason (R) is false.
Assertion (A) is false but Reason (R) is true.
Chapter:
Assertion (A): `sqrt2(5 - sqrt2)` is an irrational number.
Reason (R): Product of two irrational number is always irrational.
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
Assertion (A) is true but Reason (R) is false.
Assertion (A) is false but Reason (R) is true.
Chapter:
The point P(x, y) divides the line segment joining the points A(−1, 3) and B(9, 8) such that AP : PB = k : 1. If the coordinates of P are such that x = y, then find the value of k.
Chapter:
If Q(0, 2) is equidistant from P(5, −3) and R(x, 7), then find the value(s) of x.
Chapter:
If A(1, 1) and B(7, 9) are the end points of a diameter of a circle, then find the coordinates of the centre of the circle.
Chapter:
There are 80 cards numbered from 1 to 80. One card is drawn at random from them. Find the probability that the number on the selected card is not divisible by 8.
Chapter:
Prove that `-7 - 2sqrt3` is an irrational number, given that `sqrt3` is an irrational number.
Chapter:
Explain why (7 × 11 × 13 + 2 × 11) is not a prime number.
Chapter:
In the given figure, `angle`ABC = `angle`ACB and `(BC)/(BE) = (BD)/(AC)`.
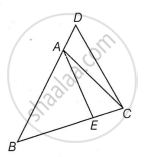
Show that `triangle`ABE ∼ `triangle`DBC and AE || DC.
Chapter:
A vessel is in the form of a hollow hemisphere surmounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
Chapter:
A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy.
Chapter:
Advertisements
Prove that (sinθ + cosecθ)2 + (cosθ + secθ)2 = 7 + tan2θ + cot2θ.
Chapter:
If cos A = `5/13`, then verify that `cosA/(1 - tanA) + sinA/(1 - cotA) = cosA + sinA`
Chapter:
The altitude of a right angled triangle is 7 cm less than its base. If its hypotenuse is 17 cm long, then represent the above information in the form of a quadratic equation.
Chapter:
The altitude of a right angled triangle is 7 cm less than its base. If its hypotenuse is 17 cm long, then find the length of the sides of the triangle.
Chapter:
Find the HCF and LCM of 260 and 910 by prime factorisation method.
Chapter:
If one zero of the polynomial x2 − 8x + k exceeds the other by 2, then find the zeroes and value of k.
Chapter:
Using graphical method, solve the following pair of equations.
x + 2y = 8 and 3x − 2y = 12
Chapter:
The sum of the digits of a 2-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
Chapter:
The marks obtained by 45 students of a class in a test are given below:
| Marks | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 | 65-70 |
| Number of students | 8 | 9 | 10 | 9 | 5 | 4 |
Find the mean and median marks.
Chapter:
The angle of elevation of a helicopter in air from a point A an the ground is 45°. After a flight of 25 sec, the angle of elevation changes to 30 °. If the helicopter is flying at a constant height of 2500 m, then find the speed of the helicopter. (Use `sqrt3` = 1.73)
Chapter:
In the given figure, AB is chord of length 6 cm of a circle of radius 5 cm. The tangents at A and B intersect at point P. Find the length of PB.
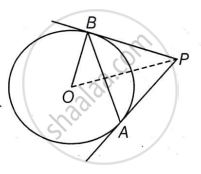
Chapter:
Prove that the parallelogram circumscribing a circle is a rhombus. Also, find the area of the rhombus, if radius of circle is 3 cm and length of one side of the rhombus is 10 cm.
Chapter:
NSS (National Service Scheme) aims to connect the students to the community and to involve them in problem solving process.
NSS symbol is based on the 'Rath' wheel of the Konark Sun Temple situated in Odisha. The wheel signifies the progress cycle of life. The diagrammatic representation of the symbol is given below
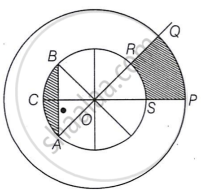
Observe the figure given above. The diameters of inner circle are equally placed. Given that OP = 21 cm and OS = 10 cm:
Based on the above information, answer the following questions:.
- Find m ∠ROS. [1]
- Find the perimeter of sector OPQ. [1]
-
- Find the area of shaded region PQRS. [2]
OR - Find the area of shaded region ACB, i.e., the segment ACB. [2]
- Find the area of shaded region PQRS. [2]
Chapter:
In the figure given below, a folding table is shown.
The legs of the table are represented by line segments AB and CD intersecting at O. Join AC and BD. Considering table top is a parallel to the ground and OB = x, OD = x + 3, OC = 3x + 19 and OA = 3x + 4, answer the following questions.
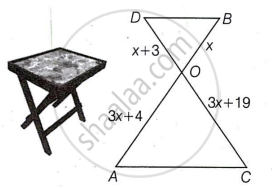
- Prove that ΔOAC is similar to ΔOBD. [1]
- Prove that `(OA)/(AC) = (OB)/(BD)`. [1]
-
- Observe the figure and find the value of x. Hence, find the length of OC. [2]
OR - Observe the figure and find `(BD)/(AC)`. [2]
- Observe the figure and find the value of x. Hence, find the length of OC. [2]
Chapter:
While preparing for a competitive examination, Akbar came across a match-stick pattern based question. The pattern is given below:
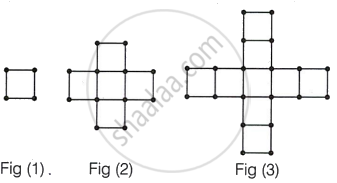
Based on the above information, answer the following questions:
- Write first term and common difference of the AP formed by number of squares in each figure. [1]
- Write first term and common difference of the AP formed by number of sticks used in each figure. [1]
-
- How many squares are there in Fig (10)? Also, write the number of sticks used in figure. (10). [2]
OR - If 88 sticks are used to make mth (fig (m)), then find the value of m. How many squares are formed in this figure? [2]
- How many squares are there in Fig (10)? Also, write the number of sticks used in figure. (10). [2]
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2023 - 2024
Previous year Question paper for CBSE Class 10 Maths-2024 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
