Question

While preparing for a competitive examination, Akbar came across a match-stick pattern based question. The pattern is given below:

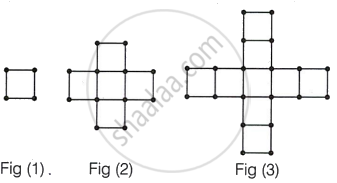
Based on the above information, answer the following questions:

1. Write first term and common difference of the AP formed by number of squares in each figure.     [1]
2. Write first term and common difference of the AP formed by number of sticks used in each figure.      [1]
3. 1. How many squares are there in Fig (10)? Also, write the number of sticks used in figure. (10).     [2]
      OR
   2. If 88 sticks are used to make mth (fig (m)), then find the value of m. How many squares are formed in this figure?     [2]

Answer 1

Given matchstick pattern:

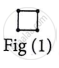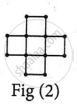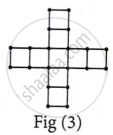Number of squares	1	5	9
Number of matchsticks	4	16	28

(i) The AP corresponding to the number of squares in each figure is 1, 5, 9, ........

First term of AP = 1

Common difference of AP = 5 − 1 = 4

(ii) The AP corresponding to the number of sticks used in each figure is 4, 16, 28 ........

First term of AP = 4

Common difference of AP = 16 − 4 = 12

(iii) 

(a) From part (i), the AP corresponding to the number of squares is 1, 5, 9, ........

Here, a = 1 and 5 − 1 = 4

We have to find a₁₀

We know that  a_n = a + (n − 1)d

= 1 + (10 − 1)4

= 1 + 9 × 4

= 37

Fig. (10) will have 37 squares.

From part (ii), the AP we get corresponding to the number of matchsticks used is 4, 16, 28, ........

Here, a = 4 and d = 16 − 4 = 12

We have to find a₁₀.

We know that a_n = a + (n − 1)d

a₁₀ = 4 + (10 − 1)12

= 4 + 9 × 12

= 4 + 108

= 112

∴ Fig. (10) will have 112 matchsticks.

OR

(b) We have given, a_m = 88

a + (m − 1)d = 88

4 + (m − 1)12 = 88  ...[∵ a = 4, d = 12]

(m − 1)12 = 84

m − 1 = 7

∴ m = 8

∴ Fig. (8) will have 88 matchsticks.

To find the number of squares in 8th figure we have to find a₈ for the AP 1, 5, 9, ........

a₈ = a + (8 − 1)d

a₈ = 1 + 7 × 4

= 29

Therefore, 8th figure will have 29 squares.