Question

The angle of elevation of a helicopter in air from a point A an the ground is 45°. After a flight of 25 sec, the angle of elevation changes to 30 °. If the helicopter is flying at a constant height of 2500 m, then find the speed of the helicopter. (Use `sqrt3` = 1.73)

Answer 1

Let A be the point on the ground and the distance CE be the distance travelled by helicopter in 25 sec.

Let AB is x and AD is y.

So, in ΔACB

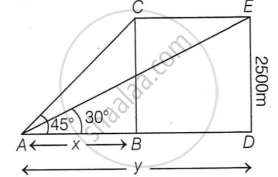
tan 45° = `(BC)/(AD) = 2500/x`

∴ 1 = `2500/x`  ...[∵ tan 45° = 1]

∴ x = 2500m 

In ΔADE,

tan 30° = `(DE)/(AD) = 2500/y`

∴ `1/sqrt3 = 2500/y`  ...[∵ tan 30° = `1/sqrt3` ]

∴ y = `2500  sqrt3`

= 2500 × 1.73  ...[Given]

∴ y = 4325 m

Distance travelled = y − x

= 4325 − 2500

= 1825 m

Speed of helicopter in 25 sec = `"Distance"/"Time"`

= `1825/25`

= 73

Hence, the speed of the helicopter is 73 m/s.