Advertisements
Advertisements
Question
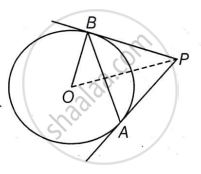
In the given figure, AB is chord of length 6 cm of a circle of radius 5 cm. The tangents at A and B intersect at point P. Find the length of PB.
Sum
Solution
Given AB = 6 cm and radius, OA = OB = 5 cm
To find Length of PA
Construction Join OA, so OA = 5 cm
OL is perpendicular to AB.
AL = LB = `6/2 = 3` ...[Since OL bisects AB]
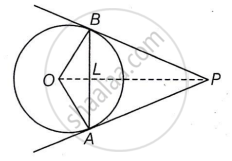
By Pythagoras theorem, in ΔOLA
OL2 + LA2 = OA2
∴ OL2 = OA2 − LA2
∴ OL2 = 52 − 32
∴ OL2 = 25 − 9
∴ OL2 = 16
∴ OL = 4 cm
We have, tan ∠AOL = `(AL)/(OL) = 3/4`
From ΔOAP,
tan ∠AOL = `(AL)/(OL)`
tan ∠AOP = `(PA)/(OA)` ...[∵ ∠AOL = ∠AOP]
`3/4 = (PA)/5`
∴ PA = `(3 xx 5)/4`
= `15/4`
= 3.75 cm
Length of PA = `15/4` = 3.75 cm
shaalaa.com
Is there an error in this question or solution?
