Question

Prove that the parallelogram circumscribing a circle is a rhombus. Also, find the area of the rhombus, if radius of circle is 3 cm and length of one side of the rhombus is 10 cm. 

Answer 1

Given ABCD, be a parallelogram circumscribing a circle with centre O.

ABCD is a rhombus.

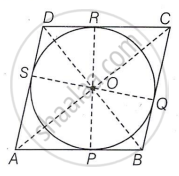
We know that the tangents drawn to a circle from an exterior point are of equal length.

∴ AP = AS, BP = BQ, CR = CQ and DR = DS

Adding the above four equations

AP + BP + CR + DR = AS + BQ + CQ + DS

(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)

∴ AB + CD = AD + BC

∴ 2AB = 2AD  ...[since AB = DC and AD = BC of parallelogram ABCD]

∴ AB = BC = DC = AD

Therefore, ABCD is a rhombus.

Join OC, OP, OQ, OR, OD, OS, OB and OA

Now, the area of rhombus = Area of ΔBOC + Area of ΔAOB + Area of ΔAOD + Area of ΔCOD

Area of ΔBOC = `1/2 xx BC xx OQ`  ...[∵ Area of triangle = `1/2 xx "Base" xx "Height"`]

= `1/2 xx 10 xx 3`

= 15 cm²

∴ Area of ΔBOC = Area of ΔAOB

= Area of ΔAOD

= Area of ΔCOD

= 15 cm²

∴ Area of rhombus = 4 × Area of ΔBOC

= 4 × 15 cm²

= 60 cm²

Therefore, the area of the rhombus is 60 cm².