Advertisements
Advertisements
Question
In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:
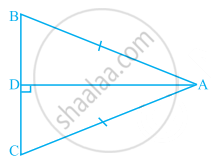
Solution
In ∆ADB and ∆ADC,
AD = AD ......(Common)
∠ADB = ∠ADC ......(Each 90°)
AB = AC ......(Given hypotenuse)
∴ ∆ADB ≅ ∆ADC ......(RHS criterion)
APPEARS IN
RELATED QUESTIONS
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, using the RHS congruence rule. In the case of congruent triangles, write the result in symbolic form:
∆ABC, ∠B = 90°, AC = 8 cm, AB = 3 cm.
∆PQR, ∠P = 90°, PR = 3 cm, QR = 8 cm.
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, using the RHS congruence rule. In the case of congruent triangles, write the result in symbolic form:
∆ABC, ∠A = 90°, AC = 5 cm, BC = 9 cm.
∆PQR, ∠Q = 90°, PR = 8 cm, PQ = 5 cm.
In Fig, DA ⊥ AB, CB ⊥ AB, and AC = BD. State the three pairs of equal parts in ∆ABC and ∆DAB. Which of the following statements is meaningful?
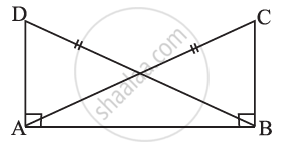
(i) ∆ABC ≅ ∆BAD
(ii) ∆ABC ≅ ∆ABD.
In Fig,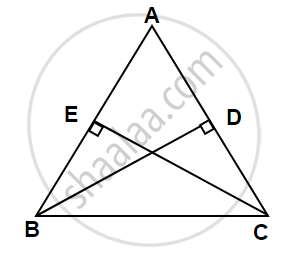
BD and CE are altitudes of ∆ABC such that BD = CE.
(i) State the three pairs of equal parts in ∆CBD and ∆BCE.
(ii) Is ∆CBD ≅ ∆BCE? Why or why not?
(iii) Is ∠DCB = ∠EBC? Why or why not?
Is ΔPRQ ≡ ΔQSP? Why?
State whether the two triangles are congruent or not. Justify your answer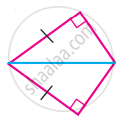
In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:

In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:
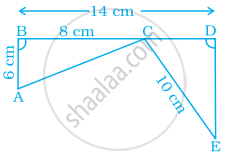
In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:
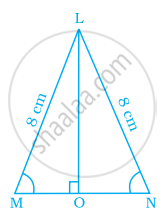
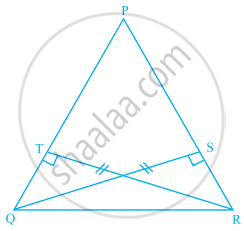
In the given figure, QS ⊥ PR, RT ⊥ PQ and QS = RT.
- Is ∆QSR = ∆RTO? Give reasons.
- Is ∠PQR = ∠PRQ? Give reasons.