Advertisements
Advertisements
Question
In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:
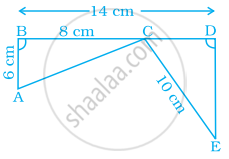
Solution
In ∆ABC, by Pythagoras theorem
(AC)2 = (AB)2 + (BC)2
(AC)2 = 62 + 82
(AC)2 = 36 + 64
(AC)2 = 100
(AC)2 = 102
∴ AC = 10 cm
In ∆EDC,
DC = BD – BC = (14 – 8) cm = 6 cm, CE = 10 cm
Now, In ∆ABC and ∆CDE,
∠B =∠D .....(Each 90°)
AB = CD = 6 cm
AC = CE = 10 cm .....(Hypotenuse)
∴ ∆ABC ≅ ∆CDE ......(RHS criterion)
APPEARS IN
RELATED QUESTIONS
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, using the RHS congruence rule. In the case of congruent triangles, write the result in symbolic form:
∆ABC, ∠A = 90°, AC = 5 cm, BC = 9 cm.
∆PQR, ∠Q = 90°, PR = 8 cm, PQ = 5 cm.
In Fig,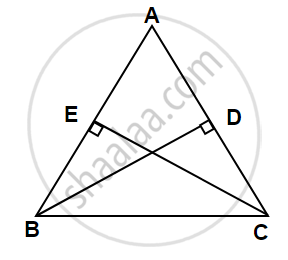
BD and CE are altitudes of ∆ABC such that BD = CE.
(i) State the three pairs of equal parts in ∆CBD and ∆BCE.
(ii) Is ∆CBD ≅ ∆BCE? Why or why not?
(iii) Is ∠DCB = ∠EBC? Why or why not?
In the given figure, D is the midpoint of OE and ∠CDE = 90°. Prove that ΔODC ≡ ΔEDC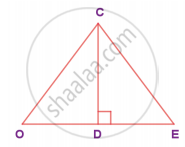
Is ΔPRQ ≡ ΔQSP? Why?
State whether the two triangles are congruent or not. Justify your answer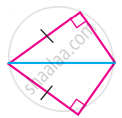
For the given pair of triangles state the criterion that can be used to determine the congruency?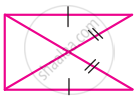
In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:
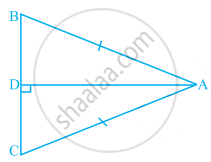
In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:

In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form:
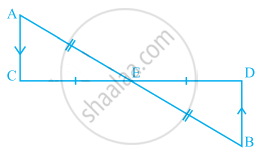
In the given pairs of triangles of the figure, using only RHS congruence criterion, determine which pairs of triangles are congruent. In congruence, write the result in symbolic form: