Advertisements
Advertisements
Question
केप्लरचे तीन नियम लिहा. त्यामुळे न्यूटनला आपला गुरुत्व सिद्धांत मांडण्यात कशी मदत झाली?
Solution
केप्लरचा पहिला नियम: ग्रहाची कक्षा ही लंब-वर्तुळाकार असून, सूर्य त्या कक्षेच्या एका नाभीवर असतो.
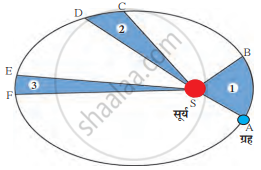
पुढील आकृतीमध्ये एका ग्रहाची सूर्याभोवतीच्या परिभ्रमणाची लंबवर्तुळाकार कक्षा दाखवली आहे. सूर्याची स्थिती S ने दाखवली आहे.
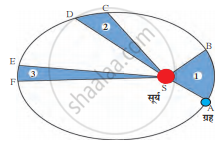
ग्रहाची सूर्याभोवतीची परिभ्रमण कक्ष (प्रारूप आकृती)
केप्लरचा दुसरा नियम: ग्रहाला सूर्याशी जोडणारी सरळ रेषा, ही समान कालावधीत समान क्षेत्रफळ व्यापन करते.
समान कालावधीत ग्रहाचे विस्थापन A → B, C → D, E → F असे होते. आकृतीमधील ASB, CSD व ESF ही क्षेत्रफळे समान आहेत.
केप्लरचा तिसरा नियम: सूर्याची परिक्रमा करणाऱ्या ग्रहाच्या आवर्तकालाचा वर्ग हा ग्रहाच्या सूर्यापासूनच्या सरासरी अंतराच्या घनाला समानुपाती असतो. म्हणजे ग्रहाचा आवर्तकाल T असेल व सूर्यापासून ग्रहाचे सरासरी अंतर r असेल, तर T2 ∝ r3 , म्हणजेच ., `"T"^2/"r"^3` स्थिर = K ......(1)
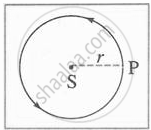
ग्रहाची सूर्याभोवतीची वर्तुळाकार गती
समजा एक वस्तू एकसमान वर्तुळाकार गतीने गतिमान आहे. अशा प्रकारे गतिमान असलेल्या वस्तूवर केंद्राकडे निर्देशित अभिकेंद्री बल प्रयुक्त होत असते, हे आपण पाहिले. या वस्तूचे वस्तुमान m ने, तिच्या कक्षेची त्रिज्या r ने व तिची चाल v ने दर्शविली तर या बलाचे परिमाण `"mv"^2/"r"` एवढे असते, हे गणिती क्रियेद्वारे दाखवता येते.
आता जर एक ग्रह वर्तुळाकार कक्षेत सूर्याची परिक्रमा करत असेल तर त्यावर सूर्याच्या दिशेने प्रयुक्त होणारे अभिकेंद्री बल F = `"mv"^2/"r"` असले पाहिजे. येथे m हे ग्रहाचे वस्तुमान, v ही त्याची चाल व r ही ग्रहाच्या वर्तुळाकार कक्षेची त्रिज्या म्हणजेच ग्रहाचे सूर्यापासूनचे अंतर आहे. त्याची चाल आपण त्याचा आवर्तकाल (T) म्हणजे सूर्याभोवती एक परिक्रमा करण्याचा कालावधी व त्रिज्या वापरून काढू शकतो.
ग्रहाने एका परिक्रमेत पार केलेले अंतर = कक्षेचा परीघ = 2πr ; r = सूर्यापासूनचे अंतर , त्यासाठी लागलेला वेळ = आवर्त काल = T
v = कक्षेचा परिघ/आवर्त काल = `(2pi"r")/"T"`
F = `"mv"^2/"r" = ("m"((2pi"r")/"T")^2)/"r" = (4 "m" pi^2 "r")/"T"^2`, ह्यास r2 ने गुणल्यावर व भागल्यावर आपल्यास मिळते की, F = `(4 "m" pi^2)/"r"^2 ("r"^3/"T"^2)` केप्लरच्या तिसऱ्या नियमा प्रमाणे `"T"^2/"r"^3` = K हे स्थिर असते. म्हणून F = `(4 "m" pi^2)/("r"^2 "K")` पण `(4"m"pi^2)/"K"` = स्थिर, म्हणून F ∝ `1/"r"^2`
म्हणजे सूर्य व ग्रह यामधील अभिकेंद्री बल, जे ग्रहाच्या परिभ्रमणास कारणीभूत असते, ते त्यांच्यामधील अंतराच्या वर्गाच्या व्यस्त प्रमाणात असते. हेच गुरुत्वीय बल असून ते अंतराच्या वर्गाच्या व्यस्त प्रमाणात असते असा न्यूटनने निष्कर्ष काढला. गुरुत्वाकर्षणाचे बल हे निसर्गातील इतर बलांच्या तुलनते अत्यंत क्षीण असते परंतु ते संपूर्ण विश्वाचे नियंत्रण करते व विश्वाचे भवितव्य निश्चित करते. ग्रह, तारे व विश्वातील इतर घटक ह्यांच्या प्रचंड वस्तुमानांमुळे हे शक्य होते.