Advertisements
Advertisements
Question
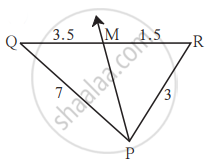
खाली त्रिकोण आणि रेषाखंडाची लांबी दिली आहे. त्यावरून आकृतीत किरण PM हा ∠QPR चा दुभाजक आहे कि नाही ते ओळखा.
Solution
ΔPQR मध्ये,
`"PQ"/"PR" = 7/3` .......(i)
`"QM"/"RM" = 3.5/1.5 = 35/15 = 7/3` .........(ii)
∴ `"PQ"/"PR" = "QM"/"RM"` .......[(i) व (ii) वरून]
∴ किरण PM हा ∠QPR चा दुभाजक आहे. .........[त्रिकोणाच्या कोनदुभाजकाच्या प्रमेयाचा व्यत्यास]]
APPEARS IN
RELATED QUESTIONS
खाली त्रिकोण आणि रेषाखंडाची लांबी दिली आहे. त्यावरून आकृतीत किरण PM हा ∠QPR चा दुभाजक आहे कि नाही ते ओळखा.
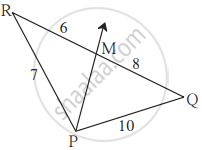
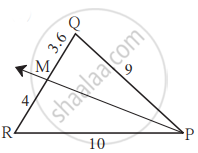
खाली त्रिकोण आणि रेषाखंडाची लांबी दिली आहे. त्यावरून आकृतीत किरण PM हा ∠QPR चा दुभाजक आहे कि नाही ते ओळखा.
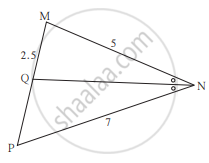
Δ MNP च्या ∠N चा NQ हा दुभाजक आहे. जर MN = 5, PN = 7, MQ = 2.5 तर QP काढा.
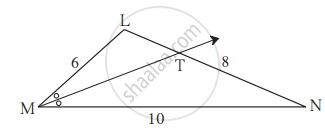
Δ LMN मध्ये किरण MT हा ∠LMN चा दुभाजक आहे. जर LM = 6, MN = 10, TN = 8 तर LT काढा.
Δ ABC मध्ये रेख BD हा ∠ABC चा दुभाजक आहे, जर AB = x, BC = x + 5, AD = x - 2, DC = x + 2 तर x ची किंमत काढा.

Δ ABC मध्ये AB = AC, ∠B व ∠C चे दुभाजक बाजू AC व बाजू AB यांना अनुक्रमे बिंदू D व E मध्ये छेदतात. तर सिद्ध करा, की रेख ED || रेख BC.
ΔPQR मध्ये रेख PM ही मध्यगा आहे. ∠PMQ व ∠PMR चे दुभाजक बाजू PQ व बाजू PR ला अनुक्रमे X आणि Y बिंदूत छेदतात, तर सिद्ध करा XY || QR.
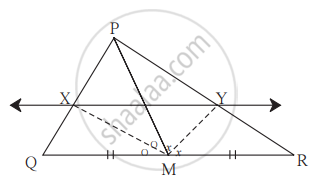
सिद्धतेतील रिकाम्या जागा भरून सिद्धता पूर्ण करा.
ΔPMQ मध्ये किरण MX हा ∠PMQ चा दुभाजक आहे.
∴ `square/square = square/square` ..... (I) (कोनदुभाजकाचे प्रमेय)
ΔPMR मध्ये किरण MY हा ∠PMR चा दुभाजक आहे.
∴ `square/square = square/square` ..... (II) (कोनदुभाजकाचे प्रमेय)
परंतु `"MP"/"MQ" = "MP"/"MR"` .....(M हा QR चा मध्य म्हणजेच MQ = MR)
∴ `"PX"/"XQ" = "PY"/"YR"`
∴ XY || QR ....(प्रमाणाच्या मूलभूत प्रमेयाचा व्यत्यास)
आकृती मध्ये ΔABC च्या ∠B व ∠C चे दुभाजक एकमेकांना X मध्ये छेदतात, रेषा AX ही बाजू BC ला Y मध्ये छेदते जर AB = 5, AC = 4, BC = 6 तर `"AX"/"XY"` ची किंमत काढा.

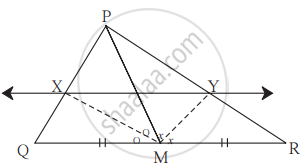
ΔPQR मध्ये रेख PM ही मध्यगा आहे. ∠PMQ व ∠PMR चे दुभाजक बाजू PQ व बाजू PR ला अनुक्रमे X आणि Y बिंदूत छेदतात. तर XY || QR सिद्ध करण्यासाठी खालील कृती पूर्ण करा.
उकल:
ΔPMQ मध्ये,
किरण MX हा ∠PMQ चा कोनदुभाजक आहे.
∴ `"MP"/"MQ" = square/square` .............(I) (कोनदुभाजकाचे प्रमेय)
ΔPMR मध्ये किरण MY हा ∠PMR चा कोनदुभाजक आहे.
∴ `"MP"/"MR" = square/square` .............(II) (कोनदुभाजकाचे प्रमेय)
परंतु `"MP"/"MQ" = "MP"/"MR"` ................(III) (M हा QR चा मध्यबिंदू आहे म्हणजेच MQ = MR)
∴ `"PX"/square = square/"YR"` ............(विधान (I), (II) व (III) वरून)
∴ XY || QR ...........(प्रमाणाच्या मूलभूत प्रमेयाचा व्यत्यास)

ΔABC मध्ये, किरण BD हा ∠ABC चा दुभाजक आहे. A - D - C, रेख DE || बाजू BC, A - E - B, तर `("AB")/("BC") = ("AE")/("EB")` हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा:
सिद्धता:
ΔABC मध्ये, किरण BD हा ∠B चा दुभाजक आहे.
∴ `square/("BC") = ("AD")/("DC")` ......(I) (`square`)
ΔABC मध्ये, DE || BC
∴ `(square)/("EB") = ("AD")/("DC")` ....(II) (`square`)
∴ `("AB")/square = square/("EB")` [(I) व (II)वरून]
