Advertisements
Advertisements
Question
किसी कार की छत से l लंबाई का कोई सरल लोलक, जिसके लोलक का द्रव्यमान M है, लटकाया गया है। कार R त्रिज्या की वृत्तीय पथ पर एकसमान चाल υ से गतिमान है। यदि लोलक त्रिज्य दिशा में अपनी साम्यावस्था की स्थिति के इधर-उधर छोटे दोलन करता है तो इसका आवर्तकाल क्या होगा?
Solution
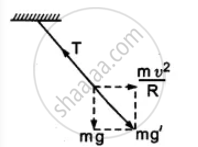
कार जब मोड़ पर मुड़ती है तो उसकी गति में त्वरण, `\frac { \upsilon ^{ 2 } }{ "R" }` (अभिकेंद्र त्वरण) होता है। इस प्रकार कार एक अजड़त्वीय निर्देश तंत्र है। इसलिए गोलक पर एक छद्म बल `\frac { "m" \upsilon ^{ 2 } }{ "R" }` वृत्तीय पथ के बाहर की ओर लगेगा जिसके कारण लोलक ऊर्ध्वाधर रहने के स्थान पर थोड़ा तिरछा हो जाएगा।
इस समय गोलक पर दो बले क्रमशः भार mg तथा अपकेंद्र बल `\frac { "m" \upsilon ^{ 2 } }{ "R" }` लगेंगे।
यदि गोलक के लिए g का प्रभावी मान g’ है तो गोलक पर प्रभावी बल mg’ होगा जो कि उक्त दो बलों का परिणामी है।
`∴ "m""g"^"'" = sqrt(("mg"^2) + (("m"upsilon^2)/"R"^2)^2)` ...`["mg" ⊥ ("m"upsilon^2)/"R"]`
अतः `"g"^"'" = sqrt("g"^2 + upsilon^4/"R"^2)`
∴ लोलक का नया आवर्तकाल `"T" = 2pisqrt("l"/"g"^"'")`
`=> "T" = 2pi sqrt("l"/["g"^2 + upsilon^4/"R"^2]^(1//2))`
APPEARS IN
RELATED QUESTIONS
चंद्रमा के पृष्ठ पर गुरुत्वीय त्वरण 1.7 ms-2 है। यदि किसी सरल लोलक का पृथ्वी के पृष्ठ पर आवर्तकाल 3.5 s है तो उसका चंद्रमा के पृष्ठ पर आवर्तकाल कितना होगा? (पृथ्वी के पृष्ठ पर g = 9.8 ms-2)
किसी सरल लोलक की गति छोटे कोण के सभी दोलनों के लिए सन्निकट सरल आवर्त गति होती है। बड़े कोणों के दोलनों के लिए एक अधिक गूढ विश्लेषण यह दर्शाता है कि का मान `2\pi \sqrt { \frac { "l" }{ "g" } }` से अधिक होता है। इस परिणाम को समझने के लिए किसी गुणात्मक कारण का चिंतन कीजिए।
गुरुत्व बल के अंतर्गत मुक्त रूप से गिरते किसी केबिन में लगे सरल लोलक के दोलन की आवृत्ति क्या होती है?
