Question

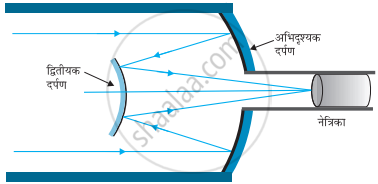
किसी कैसेग्रेन दूरबीन में चित्र में दर्शाए अनुसार दो दर्पणों का प्रयोग किया गया है। इस दूरबीन में दोनों दर्पण एक-दूसरे से 20 mm दूर रखे गए हैं। यदि बड़े दर्पण की वक्रता त्रिज्या 220 mm हो तथा छोटे दर्पण की वक्रता त्रिज्या 140 mm हो तो अनंत पर रखे किसी बिंब का अंतिम प्रतिबिंब कहाँ बनेगा?

Answer 1

कैसग्रेन दूरबीन में एक अवतल दर्पण और एक उत्तल दर्पण होता है।

दर्पणों के बीच की दूरी (अभिदृश्यक और द्वितीयक), d = 20 mm

बड़े दर्पण (अभिदृश्यक) की वक्रता त्रिज्या, R₁ = 220 mm

अतः, बड़े दर्पण की फोकस दूरी, f₁ = `"R"_1/2 = 220/2` = 110 mm

छोटे दर्पण (द्वितीयक) की वक्रता त्रिज्या, R₂ = 140 mm

अतः छोटे दर्पण की फोकस दूरी, f₂ = `"R"_2/2 = 140/2` = 70 mm

बड़े दर्पण द्वारा अनंत पर स्थित किसी वस्तु का बनाया गया प्रतिबिंब, छोटे दर्पण के लिए आभासी वस्तु का कार्य करेगा।

इसलिए, छोटे दर्पण के लिए आभासी वस्तु की दूरी, 

u = f₁ − d

= 110 − 20

= 90 mm

छोटे (द्वितीयक) दर्पण के लिए दर्पण सूत्र लागू करके, हम प्रतिबिंब दूरी (v) की गणना इस प्रकार कर सकते हैं:

`1/"v" + 1/"u" = 1/"f"_2`

`1/"v" = 1/"f"_2 - 1/"u"`

`1/"v" = 1/70 - 1/90`

`1/"v" = (90 - 70)/6300`

`1/"v" = 20/6300`

`1/"v" = 2/630`

v = `630/2`

∴ v = 315 mm

अतः छोटा दर्पण अंतिम प्रतिबिंब से 315 mm दूर बनेगा।