Advertisements
Advertisements
Question
किसी समबाहु त्रिभुज की भुजा 2a हो तो उसकी ऊँचाई ज्ञात कीजिए।
Solution
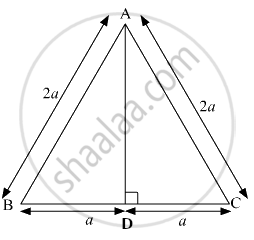
मान लो दिया गया समबाहु त्रिभुज ABC है, और रेख AD ऊँचाई है |
∠B = 60° ....(समबाहु त्रिभुज के कोण)
ΔADB में,
∠ABD + ∠BAD + ∠ADB = 180° ....(त्रिभुज के सभी कोणों का योग)
∴ 60° + ∠BAD + 90° = 180°
∴ ∠BAD + 150° = 180°
∴ ∠BAD = 180° - 150°
∴ ∠BAD = 30°
∴ ΔADB 30°-60°-90° का त्रिभुज है |
∴ त्रिभुज के 30°-60°-90° के प्रमेय से,
AD = `sqrt3/2 xx "AB"` ...(60° के सम्मुख भुजा)
∴ AD = `sqrt3/2 xx 2a`
∴ AD = `sqrt3`a
समबाहु त्रिभुज की ऊँचाई `sqrt3`a है |
APPEARS IN
RELATED QUESTIONS
आकृति में ∠MNP = 90°, रेख NQ ⊥ रेख MP, MQ = 9, QP = 4, तो NQ का मान ज्ञात कीजिए।
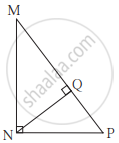
आकृति में ΔPSR में दी गई जानकारी के आधार पर RP और PS ज्ञात कीजिए।
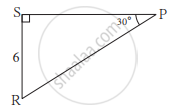
निम्नलिखित बहुवैकल्पिक प्रश्न के दिए गए उत्तरों में से उचित विकल्प चुनकर लिखिए।
ΔABC में, यदि AB = `6sqrt3` सेमी, AC = 12 सेमी और BC = 6 सेमी हो, तो ∠A का माप कितना होगा?
ΔRST में, ∠S = 90°, ∠T = 30°, RT = 12 सेमी हो तो RS तथा ST का मान ज्ञात कीजिए।
संलग्न आकृति में ΔPQR एक समबाहु त्रिभुज है जिसमें बिंदु S यह रेख QR पर इस प्रकार है कि, QS = `1/3`QR तो सिद्ध कीजिए कि; 9PS2 = 7PQ2
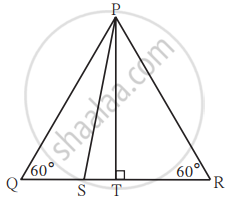
समबाहु ΔABC में आधार BC पर बिंदु P इस प्रकार है कि, PC = `1/3` BC, यदि AB = 6 सेमी तो AP ज्ञात कीजिए।
∆RST में, ∠S = 90°, ∠T = 30°, RT = 12 सेमी, तो RS का मान ज्ञात कीजिए।
