Advertisements
Advertisements
Question
किसी समलंब, जिसमें तीन भुजाएँ बराबर हैं तथा जिसकी चौथी भुजा उनमें से प्रत्येक की दोगुनी है, को ______ क्षेत्रफल के ______ समबाहु त्रिभुजों में विभाजित किया जा सकता है।
Solution
किसी समलंब, जिसमें तीन भुजाएँ बराबर हैं तथा जिसकी चौथी भुजा उनमें से प्रत्येक की दोगुनी है, को तीन क्षेत्रफल के बराबर समबाहु त्रिभुजों में विभाजित किया जा सकता है।
स्पष्टीकरण -
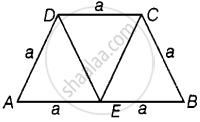
माना कि ABCD एक समलंब है, जिसमें
AD = DC = BC = a ...(कहो)
तथा AB = 2a ...[दिया गया है।]
भुजा AB पर शीर्षों D तथा C से होकर माध्यिकाएँ खींचिए।
∴ AE = EB = a
अब, समांतर चतुर्भुज ADCE में, हमें यह प्राप्त है।
AD = EC = a तथा AE = CD = a ...[समांतर चतुर्भुज में सम्मुख भुजाएँ बराबर होती हैं।]
In ΔADE तथा ΔDEC में,
AD = EC
AE = CD
तथा DE = DE ...[सामान्य]
SSS से, ΔADE = ΔDEC
त्रिभुज नियम से, ΔADE ≅ ΔDEC
इस प्रकार, ΔADE तथा ΔDEC समान भुजाओं वाले समबाहु त्रिभुज हैं।
इसी प्रकार, समांतर चतुर्भुज DEBC में, हम दिखा सकते हैं कि ΔDEC ≅ ΔECB।
अतः, समलम्ब चतुर्भुज को बराबर क्षेत्रफल वाले तीन समबाहु त्रिभुजों में विभाजित किया जा सकता है।
