Question

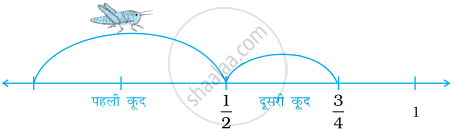
कोई कीड़ा एक संख्या रेखा के बिंदु O पर है और वह 1 की ओर उछल रहा है। वह प्रत्येक उछाल में, अपनी वर्तमान स्थिति से 1 के बीच की दूरी की आधी दूरी तय करता है। अतः, वह एक उछाल के बाद `1/2`, दो उछालों के बाद `3/4` इत्यादि पर होगा।

1. कीड़े की प्रथम 10 उछालों के बाद की स्थितियों को दर्शाने वाली एक सारणी बनाइए।
2. n उछालों के बाद कीड़ा कहाँ होगा?
3. क्या कौड़ा कभी 1 तक पहुँच पाएगा? स्पष्ट कीजिए।

Answer 1

a. प्रश्न में दी गई जानकारी के आधार पर, हम निम्नलिखित तालिका की व्यवस्था कर सकते हैं जो पहले 10 हॉप्स के लिए कीट का स्थान दिखाती है।

हॉप्स की संख्या	तय की गई दूरी	बाएँ दूरी	तय की गई दूरी
1.	`1/2`	`1/2`	`1 - 1/2`
2.	`1/2(1/2) + 1/2`	`1/4`	`1 - 1/4`
3.	`1/2(1/4) + 3/4`	`1/8`	`1 - 1/8`
4.	`1/2(1/8) + 7/8`	`1/16`	`1 - 1/16`
5.	`1/2(1/16) + 15/16`	`1/32`	`1 - 1/32`
6.	`1/2(1/32) + 31/32`	`1/64`	`1 - 1/64`
7.	`1/2(1/64) + 63/64`	`1/128`	`1 - 1/128`
8.	`1/2(1/128) + 127/128`	`1/256`	`1 - 1/256`
9.	`1/2(1/256) + 255/256`	`1/512`	`1 - 1/512`
10.	`1/2(1/512) + 511/512`	`1/1024`	`1 - 1/1024`

b. यदि हम प्रत्येक हॉप में तय की गई दूरी को देखें

पहली हॉप में तय की गई दूरी = `1 - 1/2`

दूसरी हॉप में तय की गई दूरी = `1 - 1/4`

तीसरे हॉप्स में तय की गई दूरी = `1 - 1/8`

n हॉप्स में तय की गई दूरी = `1 - (1/2)^n`

c. नहीं, क्योंकि 1 तक पहुँचने के लिए, `(1/2)^n` को कुछ परिमित n के लिए शून्य होना होगा जो संभव नहीं है।