Advertisements
Chapters
2: आंकड़ों का प्रबंधन
3: वर्ग-वर्गमूल तथा घन-घनमूल
4: एक चर वाले रैखिक समीकरण
5: चतुर्भुजों को समझना और प्रायोगिक ज्यामिति
6: ठोस आकारों का चित्रण
7: बीजीय व्यंजक, सर्वसमिकाएँ और गुणनखंडन
▶ 8: घातांक और घात
9: राशियों की तुलना
10: अनुलोम और प्रतिलोम समानुपात
11: क्षेत्रमिति
12: आलेखों का परिचय
13: संख्याओं के साथ खेलना
![NCERT Exemplar solutions for Mathematics [Hindi] Class 8 chapter 8 - घातांक और घात NCERT Exemplar solutions for Mathematics [Hindi] Class 8 chapter 8 - घातांक और घात - Shaalaa.com](/images/mathematics-hindi-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 8: घातांक और घात
Below listed, you can find solutions for Chapter 8 of CBSE NCERT Exemplar for Mathematics [Hindi] Class 8.
NCERT Exemplar solutions for Mathematics [Hindi] Class 8 8 घातांक और घात प्रश्नावली [Pages 245 - 270]
प्रश्न में, चार विकल्प दिए हैं, जिनमें से केवल एक ही सही है। सही उत्तर लिखिए।
आधार
अचर
घातांक
चर
एक निश्चित आधार 10 के लिए यदि घातांक 1 कम कर दिया जाये, तो वह संख्या बन जाती है -
पिछली संख्या का एक-दशांश
पिछली संख्या का दस गुना
पिछली संख्या का शतांश
पिछली संख्या का सौ गुना
32
`1/3^2`
`1/3^(-2)`
`-2/3`
16
8
`1/16`
`1/8`
`1/3`
3
311
3–11
`4/5`
`4/25`
`25/4`
`5/2`
`2/5`
`5/2`
`-5/2`
`-2/5`
10
100
10100
10–100
32
64
– 32
– 64
`16/81`
`81/16`
`(-16)/81`
`81/(-16)`
`(-5/9)^99`
`(5/9)^99`
`(9/(-5))^99`
`(9/5)^99`
यदि x कोई शून्येतर पूर्णांक है और m, n ऋणात्मक पूर्णांक हैं, तो xm × xn बराबर है -
xm
xm+n
xn
xm–n
यदि y कोई शून्येतर पूर्णांक है, तो y0 बराबर है -
1
0
– 1
परिभाषित नहीं
यदि x कोई शून्येतर पूर्णांक है, तो x–1 बराबर है -
x
`1/x`
– x
`(-1)/x`
यदि x कोई शून्य के अतिरिक्त पूर्णांक है और m कोई धनात्मक पूर्णांक है, तो x−m बराबर है -
xm
–xm
`1/x^m`
`(-1)/x^m`
यदि x कोई शून्य के अतिरिक्त पूर्णांक है तथा m और n कोई पूर्णांक हैं, तो (xm)n बराबर है -
xm + n
xmn
`x^(m/n)`
xm – n
निम्न में से कौन `(-3/4)^(-3)` के बराबर है?
`(3/4)^(-3)`
`-(3/4)^(-3)`
`(4/3)^3`
`(-4/3)^3`
`(5/7)^(-5)`
`(5/7)^(5)`
`(7/5)^(5)`
`(-7/5)^5`
`5/7`
`-5/7`
`7/5`
`(-7)/5`
(9)5
(9)–5
(– 9)5
(– 9)–5
किसी शून्येतर पूर्णांक x के लिए, x7 ÷ x12 बराबर है -
x5
x19
x–5
x–19
किसी शून्येतर पूर्णांक x के लिए, (x4)–3 बराबर है -
x12
x−12
x64
x−64
(7–1 – 8–1) –1 – (3–1 – 4–1) –1 का मान बराबर है -
44
56
68
12
0.000064 का मानक रूप है -
64 × 104
64 × 10–4
6.4 × 105
6.4 × 10–5
23,40,00,000 का मानक रूप है -
2.34 × 108
0.234 × 109
2.34 × 10–8
0.234 × 10–9
0.203
0.00203
203000
0.0000203
0
`1/10`
1
10
`(3/4 ÷ 5/3)^5`
`(3/4 ÷ 5/3)^1`
`(3/4 ÷ 5/3)^0`
`(3/4 ÷ 5/3)^10`
किन्हीं दो शून्येतर परिमेय संख्याओं x और y के लिए, x4 ÷ y4 बराबर है -
(x ÷ y)0
(x ÷ y)1
(x ÷ y)4
(x ÷ y)8
एक शून्येतर परिमेय संख्या p के लिए, p13 ÷ p8 बराबर है -
p5
p21
p–5
p–19
एक शून्येतर परिमेय संख्या z के लिए, (z–2)3 बराबर है -
z6
z–6
z1
z4
`1/8`
`1/16`
`-1/8`
`-1/16`
निम्न में से कौन `(2/3)^4` का व्युत्क्रम नहीं है?
`(3/2)^4`
`(3/2)^-4`
`(2/3)^-4`
`3^4/2^4`
प्रश्न 34 से 65 में, रिक्त स्थानों को भरिए, ताकि कथन सत्य हो जाएँ-
बहुत छोटी संख्याओं को मानक रूप में 10 की ______ घातों का प्रयोग करके व्यक्त किया जा सकता है।
बहुत बड़ी संख्याओं को मानक रूप में 10 की ______ घातों का प्रयोग करके व्यक्त किया जा सकता है।
(10)5 को (10)–10 सें गुणा करने पर, हमें ______ प्राप्त होता है।
`[(2/13)^-6 ÷ (2/13)^3]^3 xx (2/13)^-9` = ______ है।
[4–1 + 3–1 + 6–2]–1 का मान ______ है।
[2–1 + 3–1 + 4–1]0 = ______ है।
`(1/100000000)` का मानक रूप ______ है।
1,23,40,000 का मानक रूप ______ है।
3.41 × 106 का सामान्य रूप ______ है।
2.39461 × 106 का सामान्य रूप ______ है।
यदि 36 = 6 × 6 = 62 है, तो `1/36` आधार 6 की एक घात के रूप में ______ है।
`(5/3)^4` को ______ से गुणा करने पर, हमे 54 प्राप्त होता है।
35 ÷ 3–6 को ______ रूप में सरलीकृत किया जा सकता है।
3 × 10–7 का मान ______ है।
मानक रूप में दी हुई संख्याओं को जोड़ने के लिए, हम पहले उन्हें ______ घातांकों वाली संख्याओं में बदलते हैं।
32,50,00,00,000 का मानक रूप ______ है।
0.000000008 का मानक रूप ______ है।
2.3 × 10–10 का सामान्य रूप ______ है।
85 को ______ से भाग देने पर हमें 8 प्राप्त होता है।
______ को 2–5 से गुणा करने पर, हमें 25 प्राप्त होता है।
[3–1 × 4–1]2 का मान ______ है।
[2–1 × 3–1]–1 का मान ______ है।
(60 – 70) × (60 + 70) को सरल करने पर, हमें ______ प्राप्त होता है।
35 को ऋणात्मक घातांक के साथ लिखने के लिए व्यंजक ______ है।
(–7)6 ÷ 76 का मान ______ है।
[1–2 + 2–2 + 3–2 ] × 62 का मान ______ है।
प्रश्न 66 से 90 में, बताइए कि कथन सत्य हैं या असत्य-
(– 4)–2 का गुणन प्रतिलोम (4)–2 है।
सत्य
असत्य
`(3/2)^2` का गुणन प्रतिलोम `(2/3)^-2` के बराबर नहीं है।
सत्य
असत्य
`10^-2 = 1/100` है।
सत्य
असत्य
24.58 = 2 × 10 + 4 × 1 + 5 × 10 + 8 × 100 है।
सत्य
असत्य
329.25 = 3 × 102 + 2 × 101 + 9 × 100 + 2 × 10–1 + 5 × 10–2 है।
सत्य
असत्य
(–5)–2 × (–5)–3 = (–5)–6 है।
सत्य
असत्य
(–4)–4 × (4)–1 = (4)5 है।
सत्य
असत्य
`(2/3)^-2 xx (2/3)^-5 = (2/3)^10` है।
सत्य
असत्य
50 = 5 है।
सत्य
असत्य
(–2)0 = 2 है।
सत्य
असत्य
`(-8/2)^0 = 0` है।
सत्य
असत्य
(–6)0 = –1 है।
सत्य
असत्य
(–7)–4 × (–7)2 = (–7)–2 है।
सत्य
असत्य
`1/4^-2` का मान 16 है।
सत्य
असत्य
4–3 के लिए आधार 2 की घात के रूप का व्यंजक 26 है।
सत्य
असत्य
ap × bq = (ab)pq है।
सत्य
असत्य
`x^m/y^m = (y/x)^-m` होता है।
सत्य
असत्य
`a^m = 1/a^-m` होता है।
सत्य
असत्य
`(-2)^4 xx (5/2)^4` का घातांकीय रूप 54 है।
सत्य
असत्य
0.000037 का मानक रूप 3.7 × 10–5 है।
सत्य
असत्य
203000 का मानक रूप 2.03 × 105 है।
सत्य
असत्य
2 × 10–2 का सामान्य रूप 0.02 नहीं है।
सत्य
असत्य
5–2 का मान 25 है।
सत्य
असत्य
बड़ी संख्याओं कों 10 की धनात्मक घातों का प्रयोग करके मानक रूप में व्यक्त किया जा सकता है।
सत्य
असत्य
am × bm = (ab)m है।
सत्य
असत्य
निम्न के गुणन प्रतिलोम ज्ञात कीजिए-
100–10
निम्न के गुणन प्रतिलोम ज्ञात कीजिए-
2–2 × 2–3
निम्न के गुणन प्रतिलोम ज्ञात कीजिए-
`(1/2)^-2 ÷ (1/2)^-3`
3–5 × 3–4 को धनात्मक घातांक वाली 3 की घात के रूप में व्यक्त कीजिए।
16–2 को आधार 2 की घात के रूप में व्यक्त कीजिए।
`27/64` और `(-27)/64` को परिमेय संख्याओं की घातों के रूप में व्यक्त कीजिए।
`16/81` और `(-16)/81` को परिमेय संख्याओं के घातों के रूप में व्यक्त कौजिए।
निम्न को एक परिमेय संख्या की घात के रूप में लिखिए, जिसमें ऋणात्मक घातांक हो-
`(((-3)/2)^-2)^-3`
निम्न को एक परिमेय संख्या की घात के रूप में लिखिए, जिसमें ऋणात्मक घातांक हो-
(25 ÷ 28) × 2–7
(–2) के घन और (+4) के वर्ग का गुणनफल ज्ञात कीजिए।
सरल कीजिए -
`(1/4)^-2 + (1/2)^-2 + (1/3)^-2`
सरल कीजिए -
`(((-2)/3)^-2)^3 xx (1/3)^-4 xx 3^-1 xx 1/6`
सरल कीजिए -
`(49 xx z^-3)/(7^-3 xx 10 xx z^-5) (z ≠ 0)`
सरल कीजिए -
(25 ÷ 28) × 2–7
निम्न में x का मान ज्ञात कीजिए-
`(5/3)^-2 xx (5/3)^-14 = (5/3)^(8x)`
निम्न में x का मान ज्ञात कीजिए-
(–2)3 × (–2)–6 = (–2)2x – 1
निम्न में x का मान ज्ञात कीजिए-
(2–1 + 4–1 + 6–1 + 8–1)x = 1
293 को 10,00,000 से भाग दीजिए और परिणाम को मानक रूप में व्यक्त कीजिए।
x–3 का मान ज्ञात कीजिए, यदि x = (100)1 – 4 ÷ (100)0 है।
(–29)0 को किस संख्या से गुणा करें कि गुणनफल (+29)0 हो जाए?
(–15)–1 को किस संख्या से भाग दिया जाए कि भागफल (–15)–1 हो?
(–7)–2 ÷ (90)–1 का गुणन प्रतिलोम ज्ञात कीजिए।
यदि `5^(3x - 1) ÷ 25 = 125` हो, तो x का मान ज्ञात कीजिए।
39,00,00,000 को मानक रूप में लिखिए।
0.000005678 को मानक रूप में लिखिए।
3.2 × 106 और 4.1 × 10–1 के गुणनफल को मानक रूप में व्यक्त कीजिए।
`(1.5 xx 10^6)/(2.5 xx 10^-4)` को मानक रूप में व्यक्त कीजिए।
कुछ स्थानांतरण करने वाली चिड़िया स्वदेश की चरम जलवायु संबंधी परिस्थितियों से बचने के लिए 15000 km तक की दूरी तय करती हैं। इस दूरी को, वैज्ञानिक संकेतन का प्रयोग करते हुए मीटरों में लिखिए।
प्लूटो सूर्य से 5,91,30,00,000 m की दूरी पर है। इस दूरी को मानक रूप में व्यक्त कीजिए।
कुछ विशेष तुलाएँ 0.00000001 ग्राम तक का भार तोल सकती हैं। इस संख्या को मानक रूप में व्यक्त कीजिए।
चीनी की एक फैक्ट्री की वार्षिक बिक्री 3 बिलियन 720 मिलियन किलोग्राम है। इस बिक्री को मानक रूप में व्यक्त कीजिए।
रक्त में लाल रक्त सैलों की संख्या लगभग 5.5 मिलियन प्रति घन मिलीमीटर है। यदि औसतन शरीर में 5 लीटर रक्त होता है, तो शरीर में लाल रक्त सैलों की संख्या कितनी है? इसे मानक रूप में लिखिए। (1 लीटर = 100000 mm3 है)
निम्न को मानक रूप में व्यक्त कीजिए -
एक प्रोटोन का द्रव्यमान (ग्राम में) निम्न है
`1673/1000000000000000000000000000`
निम्न को मानक रूप में व्यक्त कीजिए -
हीलियम के एक परमाणु का व्यास 0.000000022 cm है।
निम्न को मानक रूप में व्यक्त कीजिए -
हाइड्रोजन गैस के एक अणु का द्रव्यमान लगभग 0.00000000000000000000334 टन है।
निम्न को मानक रूप में व्यक्त कीजिए -
मानव शरीर में विभिन्न आकारों और मापों वाले 1 ट्रिलियन सेल होते हैं।
निम्न को मानक रूप में व्यक्त कीजिए -
56 km को m में व्यक्त कीजिए।
निम्न को मानक रूप में व्यक्त कीजिए -
5 टन को ग्राम में व्यक्त कीजिए।
निम्न को मानक रूप में व्यक्त कीजिए -
2 वर्षों को सेकेंडों में बदलिए।
निम्न को मानक रूप में व्यक्त कीजिए -
5 हेक्टेयर को cm2 में बदलिए। (1 हेक्टेयर = 10000 m2)
x ज्ञात कीजिए, ताकि `(2/9)^3 xx (2/9)^-6 = (2/9)^(2x - 1)` हो।
`((-3)/2)^-3` को किस संख्या से भाग दिया जाए कि भागफल `((4)/27)^-2` प्राप्त हो?
यदि `6^n/6^-2 = 6^3` है, तो n का मान ज्ञात कीजिए।
यदि `(2^n xx 2^6)/2^-3 = 2^18` है, तो n का मान ज्ञात कीजिए।
`(125 xx x^-3)/(5^-3 xx 25 xx x^-6)` को सरल कीजिए।
`(16 xx 10^2 xx 64)/(2^4 xx 4^2)` को सरल कीजिए।
यदि `(5^m xx 5^3 xx 5^-2)/5^-5 = 5^12` है, तो m ज्ञात कीजिए।
एक नवजात भालू का भार 4 kg है। पाँच वर्ष की आयु के भालू का क्या भार होगा, यदि 5 वर्षों में भालू का भार पिछले भार की दूसरी घात हो जाता है?
किसी जीवाणु के सेल प्रत्येक 30 मिनट में दोगुने हो जाते हैं। कोई वैज्ञानिक केवल एक सेल से प्रारंभ करता है। निम्न समय के बाद कितने सैल हो जाएँगे?
12 घंटे
किसी जीवाणु के सेल प्रत्येक 30 मिनट में दोगुने हो जाते हैं। कोई वैज्ञानिक केवल एक सेल से प्रारंभ करता है। निम्न समय के बाद कितने सैल हो जाएँगे?
24 घंटे
ग्रह A पृथ्वी से 9.35 × 106 km की दूरी पर है तथा ग्रह B पृथ्वी से 6.27 × 107 m की दूरी पर है। कौन-सा ग्रह पृथ्वी के अधिक निकट है?
किसी जीवाणु के सेल प्रत्येक घंटे में दोगुने हो जाते हैं। यदि हम प्रारंभक रूप से 1 सेल लें, तो 8 घंटे बाद कितने सेल हो जाएँगे? उत्तर को घातों के रूप में व्यक्त कीजिए।
कोई कीड़ा एक संख्या रेखा के बिंदु O पर है और वह 1 की ओर उछल रहा है। वह प्रत्येक उछाल में, अपनी वर्तमान स्थिति से 1 के बीच की दूरी की आधी दूरी तय करता है। अतः, वह एक उछाल के बाद `1/2`, दो उछालों के बाद `3/4` इत्यादि पर होगा।
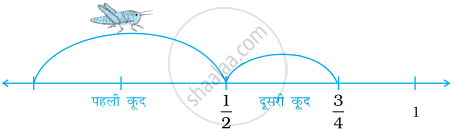
- कीड़े की प्रथम 10 उछालों के बाद की स्थितियों को दर्शाने वाली एक सारणी बनाइए।
- n उछालों के बाद कीड़ा कहाँ होगा?
- क्या कौड़ा कभी 1 तक पहुँच पाएगा? स्पष्ट कीजिए।
इकाई का अंक बताना- इस सारणी की प्रतिलिपि बनाकर इसे पूरा कीजिए और आगे आने वाले प्रश्नों के उत्तर दीजिए-
| घात सारणी | ||||||||||
| x | 1x | 2x | 3x | 4x | 5x | 6x | 7x | 8x | 9x | 10x |
| 1 | 1 | 2 | ||||||||
| 2 | 1 | 4 | ||||||||
| 3 | 1 | 8 | ||||||||
| 4 | 1 | 16 | ||||||||
| 5 | 1 | 32 | ||||||||
| 6 | 1 | 64 | ||||||||
| 7 | 1 | 128 | ||||||||
| 8 | 1 | 256 | ||||||||
| घातों की इकाइयों के अंक |
1 | 2, 4, 8, 6 | ||||||||
- बताइए कि घातों की इकाइयों के अंकों में आप क्या पैटर्न देखते हैं।
- निम्न में प्रत्येक के लिए इकाई का अंक बताइए-
- 412
- 920
- 317
- 5100
- 10500
- निम्न में प्रत्येक के लिए इकाई का अंक बताइए-
- 3110
- 1210
- 1721
- 2910
खगोलविज्ञान -
निम्न सारणी हमारे सौर मंडल में ग्रहों तथा सूर्य और चंद्रमा के द्रव्यमान दर्शाती है -
| खिगोलीय पिंड | द्रव्यमान ( किग्रा में ) | मानक संकेतन में द्रव्यमान ( किग्रा में )| |
| सूर्य | 1,990,000,000,000,000,000,000,000,000,000 | 1.99 × 1030 |
| बुध | 330,000,000,000,000,000,000,000 | |
| शुक्र | 4,870,000,000,000,000,000,000,000 | |
| पृथ्वी | 5,970,000,000,000,000,000,000,000 | |
| मंगल | 642,000,000,000,000,000,000,000,000,000 | |
| बृहस्पति | 1,900,000,000,000,000,000,000,000,000 | |
| शनि | 568,000,000,000,000,000,000,000,000 | |
| यूरेनस | 86,800,000,000,000,000,000,000,000 | |
| नेष्चून | 102,000,000,000,000,000,000,000,000 | |
| प्लूटो | 12,700,000,000,000,000,000,000 | |
| चंद्रमा | 73,500,000,000,000,000,000,000 |
- प्रत्येक ग्रह और चंद्रमा का द्रव्यमान वैज्ञानिक संकेतन में लिखिए।
- ग्रहों और चंद्रमा को द्रव्यमान के अनुसार छोटे से बड़े क्रम में लिखिए।
- किस ग्रह का द्रव्यमान लगभग वही है जो पृथ्वी का है?
सौर मंडल की खोज -
नीचे दी गई सारणी सूर्य से प्रत्येक ग्रह की औसत दूरी दर्शाती है -
| ग्रह | सूर्य से दूरी (km में) | सूर्य से दूरी (km में) मानक संकेतन |
| पृथ्वी | 149,600,000 | 1.496 × 108 |
| बृहस्पति | 778,300,000 | |
| मंगल | 227,900,000 | |
| बुध | 57,900,000 | |
| नेप्चून | 4,497,000,000 | |
| प्लूटो | 5,900,000,000 | |
| शनि | 1,427,000,000 | |
| यूरेनस | 2,870,000,000 | |
| शुक्र | 108,200,000 |
- सूर्य से प्रत्येक ग्रह की दूरी को वैज्ञानिक संकेतन में व्यक्त कर सारणी को पूरा कीजिए।
- सूर्य के निकट से सूर्य के दूर होने वाले क्रम में ग्रहों को व्यवस्थित कीजिए।
यह सारणी पाँच रासायनिक तत्वों एक परमाणु के द्रव्यमान को प्रदर्शित करती है। इसका प्रयोग करते हुए, आगे आने वाले प्रश्नों के उत्तर दीजिए-
| तत्व | परमाणु का द्रव्यमान (kg में) |
| टिटेनियम | 7.95 × 10–26 |
| लेड (सीसा) | 3.44 × 10–25 |
| सिलवर (चाँदी) | 1.79 × 10–25 |
| लीथियम | 1.15 × 10–26 |
| हाइड्रोजन | 1.674 × 10–27 |
- कौन-सा तत्व सबसे अधिक भारी है?
- सिल्वर या टिटेनियम में से कौन-सा तत्व हल्का है?
- सभी पाँचों तत्वों को हल्के से भारी के क्रम में व्यवस्थित कीजिए।
ग्रह यूरेनस सूर्य से लगभग 2896819200000 मीटर दूर है। यह दूरी मानक रूप में क्या है?
एक इंच लगभग 0.02543 मीटर है। इसको मानक रूप में लिखिए।
पृथ्वी का आयतन सूर्य के आयतन का लगभग 7.67 × 10–7 गुना है। इस संख्या को सामान्य रूप में व्यक्त कीजिए।
एक इलेक्ट्रॉन का द्रव्यमान लगभग 9.1093826 × 10–31 kg है। ग्राम में यह द्रव्यमान क्या है?
20वीं शताब्दी के अंत में, विश्व की जनसंख्या लगभग 6.1 × 109 थी। इस जनसंख्या को सामान्य रूप में व्यक्त कीजिए। आप इस संख्या को शब्दों में किस प्रकार बोलेंगे?
अपने परिवार के इतिहास का अध्ययन करने के लिए शिखा ने अपने पूर्वजों की पिछली 12 पीढ़ियों का रिकार्ड खोज लिया। उसने पता किया कि पिछली 12 पीढ़ियों में उसके कितने पूर्वज थे। इस संख्या को जानने के लिए, उसने एक आरेख बनाना प्रारंभ किया। कुछ समय बाद, आरेख जटिल होने लगा।
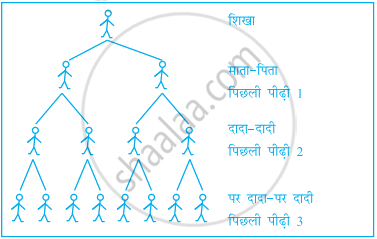
- 12 पीढ़ियों में से प्रत्येक में पूर्वजों की संख्या दर्शने के लिए एक सारणी और आलेख बनाइए।
- एक दी हुई पीढ़ी n के पूर्वजों की संख्या के लिए एक समीकरण लिखिए।
किसी नदी से होकर प्रत्येक दिन लगभग 230 बिलियन लीटर पानी बहता है। एक सप्ताह में इस नदी से होकर कितने लीटर पानी बहता है? एक वर्ष में, इस नदी से होकर कितने लीटर पानी बहता है? अपने उत्तर वैज्ञानिक संकेतन में लिखिए।
एक अर्ध जीवनकाल का अर्थ है कि एक रेडियोधर्मी पदार्थ को अपनी प्रारंभिक राशि से आधी राशि तक क्षय होने में कितना समय लगता है।
मान लीजिए कि रेडियोधर्मी क्षय के कारण किसी पदार्थ का 300 ग्राम 3 अर्ध जीवनकालों में घट कर 300 × 2–3 ग्राम रह जाता है। यह ज्ञात करने के लिए कि कितना पदार्थ बचा है, 300 × 2–3 का मान निकालिए।
स्पष्ट कीजिए कि क्यों व्यंजक 300 × 2–n का n अर्ध-जीवनकालों के बाद शेष बची पदार्थ की मात्रा ज्ञात करने के लिए किया जा सकता है।
किसी रेडियोधर्मी पदार्थ की एक मात्रा पर विचार कौजिए। व्यंजक 3–t का उपयोग t अर्ध-जीवनकालों के बाद इस मात्रा के शेष भाग को ज्ञात करने में किया जा सकता है। उस पदार्थ का कितना भाग 7 अर्ध-जीवनकालों के बाद शेष रहता है?
किसी रेडियोधर्मी पदार्थ की एक मात्रा पर विचार कौजिए। व्यंजक 3–t का उपयोग t अर्ध-जीवनकालों के बाद इस मात्रा के शेष भाग को ज्ञात करने में किया जा सकता है। कितने अर्ध-जीवनकालों के बाद प्रारंभिक मात्र का `1/243` भाग शेष रहता है?
एक फर्मी 10–15 मीटर के बराबर है। एक प्रोटॉन की त्रिज्या 1.3 फर्मीस है। एक प्रोटॉन की मीटरों में त्रि्या को मानक रूप में लिखिएं।
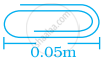
नीचे दिये गए पेपरक्लिप की लंबाई दर्शाई गयीं है। लंबाई मानक रूप में कितनी है?
घातांकों के गुणों का प्रयोग करते हुए, सत्यापित कीजिए कि कथन सत्य है?
`1/4(2^n) = 2^(n - 2)`
घातांकों के गुणों का प्रयोग करते हुए, सत्यापित कीजिए कि कथन सत्य है?
`4^(n - 1) = 1/4(4)^n`
घातांकों के गुणों का प्रयोग करते हुए, सत्यापित कीजिए कि कथन सत्य है?
25(5n – 2) = 5n
रिक्त स्थानों को भरिए-

एक दिन में 86,400 सेकेंड होते हैं। एक सेकेंड कितने दिन लंबा है? अपने उत्तर को वैज्ञानिक संकेतन में व्यक्त कीजिए।
नीचे दी हुई सारणी किसी राज्य के 2008 और 2009 वर्षों में विभिन्न फसल उत्पादनों को दर्शाती है। इस सारणी को देखिए और आगे आने वाले प्रश्नों के उत्तर दीजिए।
| फसल | 2008 का उत्पादन ( हेक्टेयर ) |
2009 के उत्पादन में वृद्धि / कमी ( हेक्टेयर ) |
| बाजरा | 1.4 × 103 | – 100 |
| ज्वार | 1.7 × 106 | – 440,000 |
| चावल | 3.7 × 103 | – 100 |
| गेहूँ | 5.1 × 105 | + 190,000 |
- किस (किन) फसल (लों) के उत्पादन में कमी हुई?
- वर्ष 2009 में हुए सभी फसलों के उत्पादनों को मानक रूप में व्यक्त कीजिए।
- यह कल्पना करते हुए कि, चावल के उत्पादन में प्रत्येक वर्ष उतनी हीं कमी होगी जितनी 2009 में हुई है, तो 2015 में कितने हेक्टेयर भूमि में चावल का उत्पादन होगा? इसे मानक रूप में लिखिए।
खींचने वाली मशीन
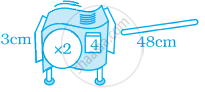
मान लीजिए कि आपके पास एक खींचने वाली मशीन है, जो अधिकांश वस्तुओं को खींचकर बड़ा कर सकती है। उदाहरणार्थ, यदि आप एक (× 4) खींचने वाली मशीन में एक 5 मीटर लंबी डंडी डालते हैं, तो वह ( नीचे के अनुसार ) परिणाम देती है। आप 20 मीटर लंबी डंडी प्राप्त करेंगे। अब आप यदि आप (× 4) मशीन में 10 सेमी लंबी गाजर डालें, तो बाहर निकलने पर इसकी क्या लंबाई होगी?

दो मशीनों को जोड़ा जा सकता है। यदि इन जोड़ी गयी मशीनों में कुछ डाला जाता है, तो पहली मशीन का निर्गम दूसरी मशीन का आगमन होता है। कौन-सी दो मशीनें मिलकर वहीं कार्य करती हैं जो एक मशीन (× 102) कार्य करती है? क्या दो मशीनों की एक से अधिक ऐसी व्यवस्थाएँ हैं?
दो मशीनों को जोड़ा जा सकता है। यदि इन जोड़ी गयी मशीनों में कुछ डाला जाता है, तो पहली मशीन का निर्गम दूसरी मशीन का आगमन होता है। कौन-सी खींचने वाली मशीन उतना ही कार्य करेगी जितना दो (× 2) मशीनें मिलकर करती हैं?
  |
रिपीटर मशीन
इसी प्रकार, रिपीटर मशीन एक परिकल्पित मशीन है, जो स्वत: ही वस्तुओं को बार-बार आवर्धित करती रहती है। उदाहरणार्थ, किसी तार को एक (× 24) मशीन में भेजने का अर्थ वही है, जो उसे एक (× 2) मशीन में चार बार भेजने का है। अतः, यदि आप तार के एक 3 सेमी टुकड़े को एक (× 24) मशीन में भेजते हैं, तो उसकी लंबाई 3 × 2 × 2 × 2 × 2 = 48 सेमी हो जाएगी। इसें इस प्रकार भी लिखा जा सकता है कि आधार 2 की मशीन को 4 बार अनुप्रयोगित किया गया है।
इस मशीन में 4 सेमी लंबी पट्टी डालने पर उसकी नयी लंबाई क्या होगी?
निम्न रिपीटर मशीनों में से प्रत्येक में, आधार मशीन का कितनी बार प्रयोग किया गया है तथा लंबाई में कुल खिंचाव कितना है?
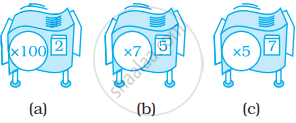
ऐसी तीन रिपीटर मशीनें ज्ञात कीजिए, जो उतना ही कार्य करेंगी जो एक (× 64) मशीन करती है। इन्हें खींचिए या इन्हें घातांकों का प्रयोग करते हुए स्पष्ट कौजिए।
निम्न मशीन 2 सेमी लंबी एक चॉक का क्या करेगी?
0 घातांक वाली एक रिपीटर मशीन में आधार मशीन का 0 बार प्रयोग किया जाता है। ये मशीनें एक चॉक के टुकड़े का क्या करेंगी?

घातांक वाली एक रिपीटर मशीन में आधार मशीन का 0 बार प्रयोग किया जाता है। आप 60 के मान के बारे में क्या सोचते हैं?
सिकोड़ने वाली मशीन-
सिकोड़ने वाली मशीन में, एक डंडी को दबा कर उसकी लंबाई कम की जाती है। यदि नीचे दी गई सिकोड़ने वाली मशीन में एक 9 cm लंबी सैंडविच रखी जाएगी, तो यह बाहर निकलने पर कितनी लंबी होगी?

जब 1 cm लंबे कीड़े को निम्न मशीनों के संग्रह में डालते हैं, तो कया होता है -

जब 1 cm लंबे कीड़े को निम्न मशीनों के संग्रह में डालते हैं, तो कया होता है -
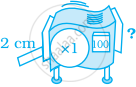
संचय ने गोंद की 1 cm लंबी पट्टी को एक (1 × 3–2) मशीन में डाला। बाहर निकलने पर यह पट्टी कितनी लंबी थी?
अजय के पास 1 cm लंबा एक गोंद की पट्टी का टुकड़ा था। उसने उसे नीचे दी हुई रिपीटर मशीन में डाल दिया और यह बाहर निकलने पर `1/(100,000)` cm लंबा था। आकृति में अज्ञात मान क्या है?

एक अकेली मशीन ज्ञात कीजिए, जो वही कार्य करे, जो मशीनों के निम्न संग्रह करते हैं -
एक (× 23) मशीन के बाद एक (× 2–2) मशीन
एक अकेली मशीन ज्ञात कीजिए, जो वही कार्य करे, जो मशीनों के निम्न संग्रह करते हैं -
एक (× 24) मशीन के बाद एक `(xx (1/2)^2)` मशीन
एक अकेली मशीन ज्ञात कीजिए, जो वही कार्य करे, जो मशीनों के निम्न संग्रह करते हैं -
एक (× 599) मशीन के बाद एक (5–100) मशीन
एक ऐसी अकेली रिपीटर मशीन ज्ञात कीजिए, जो उतना ही कार्य करेगी जितना नीचे दी गयी मशीनों संग्रह करता है -
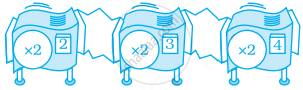
एक ऐसी अकेली रिपीटर मशीन ज्ञात कीजिए, जो उतना ही कार्य करेगी जितना नीचे दी गयी मशीनों संग्रह करता है -
एक ऐसी अकेली रिपीटर मशीन ज्ञात कीजिए, जो उतना ही कार्य करेगी जितना नीचे दी गयी मशीनों संग्रह करता है -

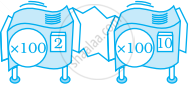
एक ऐसी अकेली रिपीटर मशीन ज्ञात कीजिए, जो उतना ही कार्य करेगी जितना नीचे दी गयी मशीनों संग्रह करता है -
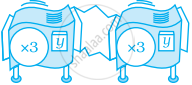
एक ऐसी अकेली रिपीटर मशीन ज्ञात कीजिए, जो उतना ही कार्य करेगी जितना नीचे दी गयी मशीनों संग्रह करता है -

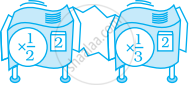
एक ऐसी अकेली रिपीटर मशीन ज्ञात कीजिए, जो उतना ही कार्य करेगी जितना नीचे दी गयी मशीनों संग्रह करता है -
मशीनों के संग्रह के लिए, निर्धारित कीजिए कि क्या कोई ऐसी अकेली रिपीटरं मशीन है जो वही कार्य करेगी जो यह संग्रह करता है। यदि हाँ तो इसका विवरण दीजिए या इसकी आकृति खींचिए।
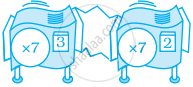
मशीनों के संग्रह के लिए, निर्धारित कीजिए कि क्या कोई ऐसी अकेली रिपीटरं मशीन है जो वही कार्य करेगी जो यह संग्रह करता है। यदि हाँ तो इसका विवरण दीजिए या इसकी आकृति खींचिए।
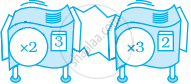
मशीनों के संग्रह के लिए, निर्धारित कीजिए कि क्या कोई ऐसी अकेली रिपीटरं मशीन है जो वही कार्य करेगी जो यह संग्रह करता है। यदि हाँ तो इसका विवरण दीजिए या इसकी आकृति खींचिए।

मशीनों के संग्रह के लिए, निर्धारित कीजिए कि क्या कोई ऐसी अकेली रिपीटरं मशीन है जो वही कार्य करेगी जो यह संग्रह करता है। यदि हाँ तो इसका विवरण दीजिए या इसकी आकृति खींचिए।
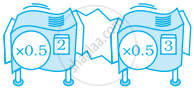
मशीनों के संग्रह के लिए, निर्धारित कीजिए कि क्या कोई ऐसी अकेली रिपीटरं मशीन है जो वही कार्य करेगी जो यह संग्रह करता है। यदि हाँ तो इसका विवरण दीजिए या इसकी आकृति खींचिए।
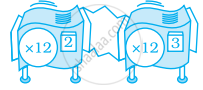
शिखा को एक गोल्फ कोर्स डिजाइनर से एक (× 23) मशीन द्वारा और फिर एक (× 33) मशीन द्वारा ताड़ के पेड़ लगाने का आर्डर प्राप्त होता है। वह सोचती है कि वह इस कार्य को एक अकेली रिपीटर मशीन से कर सकती है। उसे किस अकेली रिपीटर मशीन का प्रयोग करना चाहिए?
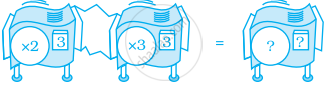
नेहा को कुछ स्टिक्स को उनकी मूल लंबाइयों से 252 गुना खींच कर लंबा करवाना है, परंतु उसकी (× 25) मशीन टूट जाती है। दो रिपीटर मशीनों का संग्रह ज्ञात कीजिये जो (× 25) मशीन के समान ही कार्य कर सके। इसको प्रारंभ करने के लिए, आप एक ऐसे संग्रह के बारे में सोचिए जिसे आप एक (× 25) मशीन के बदले में प्रयोग कर सकते हैं।

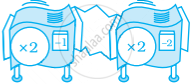
आरेख के लिए, अज्ञात सूचना की पूर्ति कीजिए।
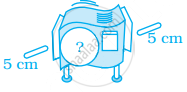
आरेख के लिए, अज्ञात सूचना की पूर्ति कीजिए।
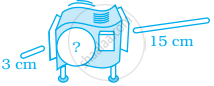
आरेख के लिए, अज्ञात सूचना की पूर्ति कीजिए।
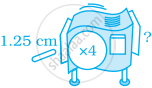
आरेख के लिए, अज्ञात सूचना की पूर्ति कीजिए।
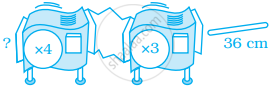
यदि संभव है, तो अभाज्य संख्या के आधार वाली मशीनों का एक संग्रह ज्ञात कीजिए, जो वही कार्य करे जो एक दी हुई खींचने वाली मशीन करती है। (× 1) मशीन का प्रयोग मत कीजिए।

यदि संभव है, तो अभाज्य संख्या के आधार वाली मशीनों का एक संग्रह ज्ञात कीजिए, जो वही कार्य करे जो एक दी हुई खींचने वाली मशीन करती है। (× 1) मशीन का प्रयोग मत कीजिए।

यदि संभव है, तो अभाज्य संख्या के आधार वाली मशीनों का एक संग्रह ज्ञात कीजिए, जो वही कार्य करे जो एक दी हुई खींचने वाली मशीन करती है। (× 1) मशीन का प्रयोग मत कीजिए।

यदि संभव है, तो अभाज्य संख्या के आधार वाली मशीनों का एक संग्रह ज्ञात कीजिए, जो वही कार्य करे जो एक दी हुई खींचने वाली मशीन करती है। (× 1) मशीन का प्रयोग मत कीजिए।

ऐसी दो रिपीटर मशीनें ज्ञात कीजिए, जो वही कार्य करें जो एक (× 81) मशीन करती है।
एक रिपीटर मशीन ज्ञात कीजिए, जो वही कार्य करे जो एक `(xx 1/8)` मशीन कार्य करती है।
ऐसी तीन मशीनें ज्ञात कीजिए, जो (× 5) मशीनों के संग्रहों से बदली जा सकती हैं।
नीचे दिये गये चार्ट के बाएँ स्तंभ में रिव्बन के निवेश टुकड़ों की लंबाइयाँ दी गयी हैं। खींचने वाली मशीनें ऊपर दी गयी हैं। अन्य प्रविष्टियाँ उस पंक्ति द्वारा रिव्बन को उस स्तंभ में दी गयी मशीन में निवेश करने से प्राप्त निर्गतों की हैं। इसकी प्रतिलिपि बनाकर पूरा कीजिए -
| निवेश लंबाई | मशीन | ||
| × 2 | |||
| 1 | 5 | ||
| 3 | |||
| 14 | 35 | ||
नीचे दिये गये चार्ट के बाएँ स्तंभ में सोने की प्रवेश जंजीरों की लंबाइयाँ दी गयी हैं तथा रिपीटर मशीनों को ऊपर लिखा गया है। अन्य प्रविष्टियाँ उन निर्गतों के लिए हैं जो उस पंक्ति में से दिये गये जंजीर के निवेश द्वारा उस स्तंभ में दी रिपीटर मशीन द्वारा प्राप्त होते हैं। इसकी प्रतिलिपि बनाकर इसे पूरा कीजिए।
| निवेश लंबाई | रिपीटर मशीन | ||
| × 23 | × 33 | ||
| 40 | 125 | ||
| 2 | 50 | ||
| 162 | |||
बहुत समय पहले, प्राचीन काल में, एक किसान ने एक राजा की पुत्री की जान बचाई। राजा ने किसान को उसकी इच्छानुसार पुरस्कार देने का निर्णय किया। वह किसान, जो शतरंज का एक चैंपियन था, ने एक असामान्य प्रार्थना की जो इस प्रकार है -
“मैं चाहता हूँ कि आप 1 रुपया मेरे शतरंज के बोर्ड के पहले वर्ग पर रखें, 2 रुपए दूसरे वर्ग पर, 4 रुपए तीसरे वर्ग पर, 8 रुपए चौथे वर्ग पर, और इसी प्रकार आगे रखते जाएँ, जब तक कि सभी 64 वर्गों पर रुपए न रख दिए जाएँ। प्रत्येक वर्ग में उस वर्ग से पहले वर्ग में रखे रुपयों के दुगुने रुपए रखे होने चाहिए।'' राजा ने सोचा कि यह राशि बहुत कम है। इसलिए उसने किसान से कोई अच्छा पुरस्कार माँगने के लिए कहा। परंतु किसान उससे सहमत नहीं हुआ।
क्या आप सोचते हैं कि किसान का चुनाव बुद्धिमतापूर्ण था?
(संकेत- निम्न सारणी आपको यह जानने में सहायता कर सकती है कि कौन सा वर्ग प्रथम होगा 'जिस पर राजा न्यूनतम 10 लाख रुपए रखेगा।)
| शतरंज के बोर्ड पर वर्ग की संख्या |
धनराशि ( रुपयों में ) |
| पहला वर्ग | 1 |
| दूसरा वर्ग | 2 |
| तीसरा वग | 4 |
सूर्य का व्यास 1.4 × 109 m है तथा पृथ्वी का व्यास 1.2756 × 107 m है। विभाजन द्वारा इन व्यासों की तुलना कीजिए।
मंगल का द्रव्यमान 6.42 × 1029 kg है और सूर्य का द्रव्यमान 1.99 kg × 1030 kg है। उनका कुल द्रव्यमान क्या है?
सूर्य और पृथ्वी के बीच की दूरी 1.496 × 108 km है तथा पृथ्वी और चंद्रमा के बीच की दूरी 3.84 × 108 m है। सूर्य ग्रहण होने पर, चंद्रमा पृथ्वी और सूर्य के बीच में आ जाता है। इस विशेष समय पर सूर्य और चंद्रमा के बीच की दूरी कया है?
एक विशेष तारा पृथ्वी से 8.1 × 1013 km की दूरी पर हैं। यह निश्चित रखते हुए कि प्रकाश 3 × 108 m प्रति सैकेंड के वेग से चलता है। ज्ञात कीजिए कि प्रकाश उस तारे से पृथ्वी तक पहुँचने में कितना समय लेता है।
(–15)–1 को किस संख्या से भाग दिया जाये कि भागफल (–5)–1 प्राप्त हो जाये?
(–8)–3 को किस संख्या से गुणा करें कि गुणनफल (–6)–3 प्राप्त हो जाये?
निम्न में x ज्ञात कीजिए -
`(- 1/7)^-5 ÷ (- 1/7)^-7 = (-7)^x`
निम्न में x ज्ञात कीजिए -
`(2/5)^(2x + 6) xx (2/5)^3 = (2/5)^(x + 2)`
निम्न में x ज्ञात कीजिए -
2x + 2x + 2x = 192
निम्न में x ज्ञात कीजिए -
`((-6)/7)^(x - 7) = 1`
निम्न में x ज्ञात कीजिए -
23x = 82x + 1
निम्न में x ज्ञात कीजिए -
5x + 5x – 1 = 750
यदि a = – 1 और b = 2 है, तो निम्न के मान ज्ञात कीजिए -
ab + ba
यदि a = – 1 और b = 2 है, तो निम्न के मान ज्ञात कीजिए -
ab – ba
यदि a = – 1 और b = 2 है, तो निम्न के मान ज्ञात कीजिए -
ab × ba
यदि a = – 1 और b = 2 है, तो निम्न के मान ज्ञात कीजिए -
ab ÷ ba
निम्न को घातांकी रूप में व्यक्त कीजिए -
`(-1296)/14641`
निम्न को घातांकी रूप में व्यक्त कीजिए -
`(-125)/343`
निम्न को घातांकी रूप में व्यक्त कीजिए -
`400/3969`
निम्न को घातांकी रूप में व्यक्त कीजिए -
`(-625)/10000`
सरल कीजिए -
`[(1/2)^2 - (1/4)^3]^-1 xx 2^-3`
सरल कीजिए -
`[(4/3)^-2 - (3/4)^2]^((-2))`
सरल कीजिए -
`(4/13)^4 xx (13/7)^2 xx (7/4)^3`
सरल कीजिए -
`(1/5)^45 xx (1/5)^-60 - (1/5)^(+28) xx (1/5)^-43`
सरल कीजिए -
`((9)^3 xx 27 xx t^4)/((3)^-2 xx (3)^4 xx t^2)`
सरल कीजिए -
`((3^-2)^2 xx (5^2)^-3 xx (t^-3)^2)/((3^-2)^5 xx (5^3)^-2 xx (t^-4)^3`
Solutions for 8: घातांक और घात
![NCERT Exemplar solutions for Mathematics [Hindi] Class 8 chapter 8 - घातांक और घात NCERT Exemplar solutions for Mathematics [Hindi] Class 8 chapter 8 - घातांक और घात - Shaalaa.com](/images/mathematics-hindi-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [Hindi] Class 8 chapter 8 - घातांक और घात
Shaalaa.com has the CBSE Mathematics Mathematics [Hindi] Class 8 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [Hindi] Class 8 CBSE 8 (घातांक और घात) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [Hindi] Class 8 chapter 8 घातांक और घात are बहुत बड़ी संख्याओं और बहुत छोटी संख्याओं की तुलना, घातांक, ऋणात्मक घातांकों की घात, घातांक और घातों का उपयोग दशमलव संख्या पद्धति में, ऋणात्मक घातांक और घातांक के नियम, छोटी संख्याओं को घातांकों का प्रयोग कर मानक रूप में व्यक्त करना.
Using NCERT Exemplar Mathematics [Hindi] Class 8 solutions घातांक और घात exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [Hindi] Class 8 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 8, घातांक और घात Mathematics [Hindi] Class 8 additional questions for Mathematics Mathematics [Hindi] Class 8 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
