NCERT Exemplar solutions for Mathematics [Hindi] Class 8 chapter 4 - एक चर वाले रैखिक समीकरण [Latest edition]

निम्न में से किस समीकरण का हल न तो भिन्न है और न ही पूर्णांक है?

समीकरण ax + b = 0 का हल है –

यदि 8x − 3 = 25 + 17x, तो x है –

एक पद को समीकरण के एक पक्ष से दूसरे पक्ष में ले जाना कहलाता है –

यदि `(5x)/3 - 4 = (2x)/5`, तो 2x − 7 का मान है –

x का वह मान, जिसके लिए व्यंजक 3x − 4 और 2x + 1 बराबर हो जाएँगे, है –

यदि a और b धनात्मक पूर्णांक हैं, तो समीकरण ax = b का हल सदैव ही होगा –

एक चर वाले रैखिक समीकरण में होता है –

निम्न में से कौन एक रैखिक व्यंजक है?

एक चर वाली रैखिक समीकरण का होता है / के होते हैं –

यदि `(−4)/3y = -3/4`, तो y बराबर है –

दो अंकों वाली एक संख्या के दहाई के स्थान का अंक इकाई के स्थान के अंक से 3 अधिक है। मान लीजिए कि इकाई के स्थान पर अंक b है। तब, वह संख्या है –

अर्पिता की वर्तमान आयु शिल्पा की आयु की तिगुनी है। यदि 3 वर्ष पहले शिल्पा की आयु x वर्ष थी, तो अर्पिता की वर्तमान आयु है –

7 के तीन क्रमागत गुणजों का योग 357 है। तब, इनमें सबसे छोटा गुणज है –

एक चर वाली एक रैखिक समीकरण में, उस चर का ______ ऋणेतर पूर्णांकीय घातांक 1 होता है।

समीकरण 3x − 4 = 1 − 2x का हल ______ है।

समीकरण `2y = 5y - 18/5` का हल ______ है।

चर का वह मान, जिससे एक समीकरण के दोनों पक्ष बराबर हो जाएँ, उस समीकरण का ______ कहलाता है।

9x – ______ = –21 का हल (–2) है। 

तीन क्रमागत संख्याएँ, जिनका योग 12 है, ______, ______ और ______ है।

जब ₹ 25 को A और B में इस प्रकार विभाजित किया जाता है कि A को B से ₹ 8 अधिक मिलते हैं, तो इसमें A का भाग ______ है। 

समीकरण के एक पद को दूसरे पक्ष में उसका ______ बदलकर स्थानांतरित किया जा सकता है। 

x में से 8 को घटाने पर परिणाम 2 प्राप्त होता है। तब, x का मान ______ है। 

जब किसी संख्या को 8 से भाग दिया जाता है, तो परिणाम –3 प्राप्त होता है। वह संख्या ______ है।

जब p और 4 के गुणनफल में से 9 को घटाया जाता है, तो परिणाम 11 प्राप्त होता है। तब, p का मान ______ है।

यदि `2/5x - 2 = 5 - 3/5x` है, तो x = ______।  

18 वर्ष बाद, स्वर्णिम अपनी वर्तमान आयु की चार गुनी आयु की होगी। उसकी वर्तमान आयु ______ है।

कथन "x के चार गुने में 15 जोड़ने पर 39 प्राप्त होता है" को समीकरण में बदलने पर ______ प्राप्त होता है।

एक परिमेय संख्या का हर उसके अंश x से 10 अधिक है। यदि अंश में 1 की वृद्धि की जाए तथा हर में 1 की कमी की जाए, नए हर के लिए व्यंजक ______ है।

10 के दो क्रमागत गुणजों का योग 210 है। तब, इनमें से छोटा गुणज ______ है।

3 वर्ष पहले एक लड़के की आयु y वर्ष थी। उसकी आयु 2 वर्ष पहले (y – 2) वर्ष थी।

शिखा की वर्तमान आयु p वर्ष है। रीमू की वर्तमान आयु शिखा की वर्तमान आयु की चार गुनी है। 5 वर्ष बाद, रीमू की आयु 15p वर्ष हो जाएगी। 

दो अंकों की एक संख्या की इकाई का अंक x है। यदि अंकों का योग 9 है, तो वह संख्या (10x – 9) है।

अंजू और उसकी माँ की आयु का योग 65 वर्ष है। यदि अंजू की वर्तमान आयु y वर्ष है, तो 5 वर्ष पहले उसकी माँ की आयु (60 – y) वर्ष थी।

किसी कक्षा में, लड़के और लड़कियों की संख्याओं का अनुपात 5 : 4 है। यदि लड़कों की संख्या लड़कियों की संख्या से 9 अधिक है, तो लड़कों की संख्या 9 है।

A और B की आयु का योग 90 वर्ष है। पाँच वर्ष पूर्व A और B की आयु क्रमश: (x – 5) वर्ष और (85 – x) वर्ष होगी, जहाँ x वर्ष A की वर्तमान आयु है। 

दो भिन्न-भिन्न समीकरणों का एक ही हल कभी नहीं हो सकता है।

समीकरण 3x – 3 = 9 में, –3 का RHS में स्थानापन्न करने पर, हमें 3x = 9 प्राप्त होता है।

समीकरण 2x = 4 – x में, – x का LHS में स्थानापन्न करने पर, हमें x = 4 प्राप्त होता है।

यदि `15/8 - 7x = 9` है, तो `-7x = 9+15/8` है। 

यदि `x/3 + 1 = 7/15` है, तो `x/3 = 6/15` है। 

यदि 6x = 18 है, तो 18x = 54 है।

यदि `x/11 = 15` है, तो `x = 11/15` है।

यदि x एक सम संख्या है, तो उससे अगली सम संख्या 2(x + 1) है।

यदि दो संख्याओं का योग 93 है और इनमें से एक x है, तो दूसरी संख्या 93 – x होगी।

दो संख्याओं का अंतर 40 है। यदि एक संख्या x है, तो दूसरी संख्या 40 – x होगी।

निम्न समीकरण को हल कीजिए–

`(3x-8)/(2x) = 1`

निम्न समीकरण को हल कीजिए–

`(5x)/(2x-1) = 2`

निम्न समीकरण को हल कीजिए–

`(2x-3)/(4x + 5) = 1/3`

निम्न समीकरण को हल कीजिए–

`8/x = 5/(x - 1)`

निम्न समीकरण को हल कीजिए–

`(5(1 - x) + 3(1 + x))/(1 - 2x) = 8`

निम्न समीकरण को हल कीजिए–

`(0.2x + 5)/(3.5x - 3) = 2/5`

निम्न समीकरण को हल कीजिए–

`(y - (4 - 3y))/(2y - (3 + 4y)) = 1/5`

निम्न समीकरण को हल कीजिए–

`x/5 = (x - 1)/6`

निम्न समीकरण को हल कीजिए–

5(x – 1) – 2(x + 8) = 0

निम्न समीकरण को हल कीजिए–

`x/2 - 1/4(x - 1/3) = 1/6(x + 1) + 1/12`

निम्न समीकरण को हल कीजिए–

`1/2(x + 1) + 1/3(x - 1) = 5/12(x - 2)`

निम्न समीकरण को हल कीजिए–

`(x + 1)/4 = (x - 2)/3`

निम्न समीकरण को हल कीजिए–

`(2x - 1)/5 = (3x + 1)/3`

निम्न समीकरण को हल कीजिए–

1 – (x – 2) – [(x – 3) – (x – 1)] = 0

निम्न समीकरण को हल कीजिए–

`3x - (x - 2)/3 = 4 - (x - 1)/4`

निम्न समीकरण को हल कीजिए–

`(3t + 5)/4 - 1 = (4t - 3)/5`

निम्न समीकरण को हल कीजिए–

`(2y - 3)/4 - (3y - 5)/2 = y + 3/4`

निम्न समीकरण को हल कीजिए–

0.25(4x – 5) = 0.75x + 8

निम्न समीकरण को हल कीजिए–

`(9 - 3y)/(1 - 9y) = 8/5`

निम्न समीकरण को हल कीजिए–

`(3x + 2)/(2x - 3) = - 3/4`

निम्न समीकरण को हल कीजिए–

`(5x + 1)/(2x) = - 1/3`

निम्न समीकरण को हल कीजिए–

`(3t - 2)/3 + (2t + 3)/2 = t + 7/6`

निम्न समीकरण को हल कीजिए–

`m - (m - 1)/2 = 1 - (m - 2)/3`

राधा एक टोकरी में कुछ फूल लेकर एक के बाद एक तीन मंदिरों में जाती है। वह प्रत्येक मंदिर में टोकरी के फूलों के आधे फूल चढ़ाती जाती है। यदि अंत में उसके पास 3 फूल शेष रह जाते हैं, तो ज्ञात कीजिए कि उसके पास प्रारंभ में कितने फूल थे।

₹ 13500 को सलमा, किरन और जेनिफर में इस प्रकार वितरित किया जाता है कि सलमा को किरन से ₹ 1000 अधिक मिलते हैं तथा जेनिफर को किरन से ₹ 500 अधिक मिलते हैं। जेनिफर को मिलने वाली राशि ज्ञात कीजिए।

किसी टंकी में पानी का आयतन दूसरी टंकी के पानी के आयतन का दोगुना है। यदि हम पहली टंकी से 25 लीटर पानी निकाल कर दूसरी टंकी में डाल दें, तो दोनों टंकियों में पानी का आयतन बराबर हो जाता है। प्रत्येक टंकी में पानी का आयतन ज्ञात कीजिए।

अनुष्का और आरुषी मित्र हैं। इनकी जेबों में बराबर-बराबर धनराशियाँ हैं। अनुष्का अपनी धनराशि का `1/3` भाग आरुषी को उसके जन्मदिन पर उपहार के रूप में दे देती है। तब, आरुषी एक रेस्टतराँ में पार्टी देती है तथा उसके बिल का भुगतान अपनी धनराशि की आधी धनराशि देकर कर देती है। यदि आरुषी की जेब में अब 1600 रु शेष रहते हैं, तो अनुष्का द्वारा उपहार में दी गयी धनराशि ज्ञात कीजिए।

कौस्तुभ के पास 60 फूल थे। वह एक मंदिर में इनमें से कुछ फूल चढ़ाता है और पाता है कि उसके शेष फूलों और प्रारंभिक फूलों का अनुपात 3:5 है। उस मंदिर में उसके द्वारा चढ़ाए गये फूलों की संख्या ज्ञात कीजिए।

तीन क्रमागत सम संख्याओं का योग 48 है। इनमें से सबसे बड़ी संख्या ज्ञात कीजिए।

तीन क्रमागत विषम संख्याओं का योग 69 है। इनमें से अभाज्य संख्या ज्ञात कीजिए।

तीन क्रमागत संख्याओं का योग 156 है। इनमें से वह संख्या ज्ञात कीजिए जो 13 का गुणज है।

वह संख्या ज्ञात कीजिए जिसके पाँचवें भाग में 30 की वृद्धि करने पर वही प्राप्त होता है जो उसके एक चौथाई भाग में 30 की कमी करने पर प्राप्त होता है।

54 को ऐसे दो भागों में बाँटिए कि एक भाग दूसरे भाग का `2/7` हो।

दो अंकों की एक संख्या के अंकों का योग 11 है। दी हुई संख्या इसके अंकों को पलटने से बनी संख्या से 9 कम है। वह संख्या ज्ञात कीजिए।

किसी त्रिभुज की दो बराबर भुजाओं में से प्रत्येक तीसरी भुजा के तिगुने से 4 मी कम है। यदि त्रिभुज का परिमाप 55 मी है, तो उसकी भुजाएँ ज्ञात कीजिए।

12 वर्ष बाद, कंवर की आयु उसकी 4 वर्ष पहले की आयु की तीन गुनी हो जाएगी। उसकी वर्तमान आयु ज्ञात कीजिए।

अनिमा ने अपनी संपत्ति का आधा भाग अपनी पुत्री के लिए छोड़ा, एक तिहाई भाग अपने पुत्र के लिए छोड़ा तथा शेष एक शैक्षणिक संस्थान को दान में दे दिया। यदि दान दी गयी संपत्ति का मूल्य ₹ 1,00000 था, तो अनिमा के पास कुल कितनी संपत्ति थी?

यदि किसी संख्या में से `1/2` घटाया जाए और अंतर को 4 से गुणा कर दिया जाए, तो परिणाम 5 प्राप्त होता है। वह संख्या क्या है?

चार क्रमागत पूर्णांकों का योग 266 है। ये पूर्णांक क्या है?

हमीद के पास विभिन्न फलों की तीन पेटियाँ हैं। पेटी A का भार पेटी B के भार से `2 1/2` kg अधिक है और पेटी C का भार पेटी B के भार `10 1/4` kg अधिक है। तीनों पेटियों का कुल भार `48 3/4` kg है। A का भार कितने किलोग्राम है?

एक आयत का परिमाप 240 cm है। यदि इसकी लंबाई में 10% की वृद्धि हो जाए और चौड़ाई में 20% की कमी हो जाए, तो आयत का परिमाप वही रहता है। आयत की लंबाई और चौड़ाई ज्ञात कीजिए।

A की आयु B की आयु से 5 वर्ष अधिक है। 5 वर्ष पहले उनकी आयु का अनुपात 3 : 2 था। उनकी वर्तमान आयु ज्ञात कीजिए। 

यदि किसी परिमेय संख्या का अंश हर से 2 कम है, तो वह परिमेय संख्या सरलतम रूप में `1/2` हो जाती है। वह परिमेय संख्या क्या है?

दो अंकों की एक संख्या के इकाई का अंक दहाई के अंक का दोगुना है। यदि इसमें 27 जोड़ दिया जाए, तो अंक पलट जाते हैं। वह संख्या ज्ञात कीजिए।

किसी व्यक्ति को वर्ष 2008 के फरवरी मास के लिए एक टाइपिस्ट के रूप में नियुक्त किया गया। उसे ₹ 500 प्रति दिन मिलते हैं, परंतु वह जितने दिन अनुपस्थित रहता है उसकी ₹ 100 प्रतिदिन की दर से धनराशि काट ली जाती है। उसे उस माह में वेतन के रूप में ₹ 9100 प्राप्त हुए। उसने कितने दिन कार्य किया?

एक स्टीमर दो बंदरगाहों के बीच की दूरी धारा के अनुकूल 3 घंटे में तय करता है तथा वह यही दूरी धारा के प्रतिकूल चलने पर 5 घंटे में तय करता है। यदि धारा की चाल 3 किमी/घंटा है, तो स्टीमर की धारा के प्रतिकूल चाल ज्ञात कीजिए।

एक महिला ₹ 1,00000 लेकर एक बैंक में गयी। उसने कैशियर से कहा कि वह उसे ₹ 500 और ₹ 1000 वाले नोट इस धनराशि के रूप में दे। उसे कुल 175 नोट मिले। प्रत्येक प्रकार के नोटों की संख्या ज्ञात कीजिए।

किसी बस में 40 यात्री हैं, जिनमें से कुछ ₹ 3 के टिकट वाले हैं और शेष ₹ 10 के टिकट वाले हैं। इन यात्रियों से एकत्रित कुल धनराशि ₹ 295 हैं। ज्ञात कीजिए कि कितने यात्रियों के पास ₹ 3 वाली टिकट हैं।

किसी भिन्न का हर उसके अंश से 4 कम है। यदि अंश में 6 जोड़ दिया जाए, तो वह हर से तिगुना हो जाता है। वह भिन्न ज्ञात कीजिए।

एक कर्मचारी किसी कंपनी में 30 दिन के ठेके पर इस प्रतिबंध के साथ नियुक्त किया गया कि उसे प्रत्येक दिन कार्य करने के ₹ 120 मिलेंगे तथा प्रत्येक दिन नहीं कार्य करने के लिए ₹ 10 का दंड देना पड़ेगा। यदि उसे कुल ₹ 2300 प्राप्त हुए हैं, तो वह कुल कितने दिन अनुपस्थित रहा?

कुसुम ने कुछ चॉकलेट ₹ 10 प्रति चॉकलेट की दर से खरीदीं। उसने उतनी ही कैंडीस ₹ 5 प्रति कैंडीस की दर से खरीदीं। वह चॉकलेट पर 20% का लाभ अर्जित करती है तथा कैंडीस पर 8% का लाभ अर्जित करती है। दिन के अंत में, सभी चॉकलेट और कैंडीस बिक गयीं तथा उसे ₹ 240 का लाभ हुआ। खरीदी गयीं चॉकलेटों की संख्या ज्ञात कीजिए।

एक स्टीमर धारा के अनुकूल जाते हुए दो बंदरगाहों के बीच की दूरी 5 घंटे में तय करता है। जबकि वह यही दूरी धारा के प्रतिकूल जाते हुए 6 घंटे में तय करता है। यदि धारा की चाल 1 km/h है, तो शांत जल में स्टीमर की चाल ज्ञात कीजिए।

दो स्थानों A और B के बीच की दूरी 210 km है। A और B से दो कारें एक साथ विपरीत दिशाओं में चलना प्रारंभ करती हैं तथा 3 घंटे के बाद उनके बीच की दूरी 54 km है। यदि एक कार की चाल दूसरी कार की चाल से 8 km/h कम है, तो प्रत्येक कार की चाल ज्ञात कीजिए।

एक बढ़ई एक पलंग बनाने के लिए ₹ 2600 लेता है। इसमें प्रयोग की गयी सामग्री की लागत ₹ 1100 है तथा मजदूरी ₹ 200 प्रति घंटा है। बढ़ई ने कितने घंटे कार्य किया?

x के किस मान के लिए, निम्न आकार का परिमाप 77 cm है?

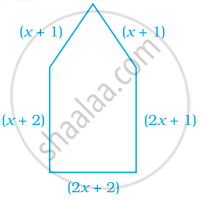
x के किस मान के लिए, निम्न आकार का परिमाप 186 cm है?

₹ 200 को A और B में इस प्रकार विभाजित करने पर कि A द्वारा प्राप्त की गयी राशि का दोगना B द्वारा प्राप्त की गयी राशि के तिगुने से ₹ 200 कम हो, B द्वारा प्राप्त की गयी राशि ज्ञात कीजिए।

मधुलिका ने एक संख्या सोची, उसका दोगुना किया और उसमें 20 जोड़ा। परिणामी संख्या को 25 से भाग देने पर उसे 4 प्राप्त होता है। वह संख्या क्या है?