Advertisements
Chapters
2: आंकड़ों का प्रबंधन
3: वर्ग-वर्गमूल तथा घन-घनमूल
4: एक चर वाले रैखिक समीकरण
5: चतुर्भुजों को समझना और प्रायोगिक ज्यामिति
6: ठोस आकारों का चित्रण
7: बीजीय व्यंजक, सर्वसमिकाएँ और गुणनखंडन
8: घातांक और घात
9: राशियों की तुलना
10: अनुलोम और प्रतिलोम समानुपात
11: क्षेत्रमिति
12: आलेखों का परिचय
13: संख्याओं के साथ खेलना
![NCERT Exemplar solutions for Mathematics [Hindi] Class 8 chapter 1 - परिमेय संख्याएँ NCERT Exemplar solutions for Mathematics [Hindi] Class 8 chapter 1 - परिमेय संख्याएँ - Shaalaa.com](/images/mathematics-hindi-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
Advertisements
Solutions for Chapter 1: परिमेय संख्याएँ
Below listed, you can find solutions for Chapter 1 of CBSE NCERT Exemplar for Mathematics [Hindi] Class 8.
NCERT Exemplar solutions for Mathematics [Hindi] Class 8 1 परिमेय संख्याएँ प्रश्नावली [Pages 9 - 26]
प्रश्न 1 से 25 में, चार विकल्प दिए हैं, जिनमें से एक सही है। सही उत्तर लिखिए।
एक संख्या, जिसे `p/q` के रूप में व्यक्त किया जा सके, जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है, कहलाती है -
प्राकृत संख्या
पूर्ण संख्या
पूर्णांक
परिमेय संख्या
`p/q` के रूप की संख्या परिमेय संख्या कहलाती है, यदि ______।
p और q पूर्णांक हैं।
p और q पूर्णांक हैं और q ≠ 0 हैं।
p और q पूर्णांक हैं और p ≠ 0 हैं।
p और q पूर्णांक हैं तथा p ≠ 0 और q ≠ 0 हैं।
संख्यात्मक व्यंजक `3/8 + ((-5))/7 = (-19)/56` दर्शाता है कि, ______
परिमेय संख्याएँ योग के अंतर्गत संवृत हैं।
परिमेय संख्याएँ योग के अंतर्गत संवृत नहीं हैं।
परिमेय संख्याएँ गुणन के अंतर्गत संवृत हैं।
परिमेय संख्याओं का योग क्रम विनिमेय नहीं है।
निम्न में से कौन सत्य नहीं है?
परिमेय संख्याएँ योग के अंतर्गत संवृत हैं।
परिमेय संख्याएँ व्यवकलन के अंतर्गत संवृत हैं।
परिमेय संख्याएँ गुणन के अंतर्गत संवृत हैं।
परिमेय संख्याएँ विभाजन के अंतर्गत संवृत हैं।
`-3/8 + 1/7 = 1/7 + ((-3)/8)` एक ऐसा उदाहरण है, जो दर्शाता है कि, ______
परिमेय संख्याओं का योग क्रम विनिमय है।
परिमेय संख्याएँ योग के अंतर्गत संवृत्त हैं।
परिमेय संख्याओं का योग सहचारी है।
परिमेय संख्याएँ योग के अंतर्गत वितरित है।
निम्न में से कौन-सा व्यंजक यह दर्शाता है कि परिमेय संख्याओं का गुणन सहचारी है?
`2/3 xx ((-6)/7 xx 3/5) = (2/3 xx (-6)/7) xx 3/5`
`2/3 xx ((-6)/7 xx 3/5) = 2/3 xx (3/5 xx (-6)/7)`
`2/3 xx ((-6)/7 xx 3/5) = (3/5 xx 2/3) xx (-6)/7`
`(2/3 xx (-6)/7)xx3/5 = ((-6)/7 xx 2/3) xx 3/5`
शून्य (0) है –
परिमेय संख्याओं के योग के लिए तत्समक
परिमेय संख्याओं के घटाने के लिए तत्समक
परिमेय संख्याओं के गुणन के लिए तत्समक
परिमेय संख्याओं के विभाजन के लिए तत्समक
एक (1) है –
परिमेय संख्याओं के योग के लिए तत्समक
परिमेय संख्याओं के घटाने के लिए तत्समक
परिमेय संख्याओं के गुणन के लिए तत्समक
परिमेय संख्याओं के विभाजन के लिए तत्समक
`(-7)/19` का योज्य प्रतिलोम है –
`(-7)/19`
`7/19`
`19/7`
`(-19)/7`
एक ऋणात्मक परिमेय संख्या का गुणन प्रतिलोम है –
एक धनात्मक परिमेय संख्या
एक ऋणात्मक परिमेय संख्या
0
1
यदि x + 0 = 0 + x = x है, जो एक परिमेय संख्या है, तो 0 कहलाता है –
परिमेय संख्याओं के योग के लिए तत्समक
x का योज्य प्रतिलोम
x का गुणन प्रतिलोम
x का व्युत्क्रम
गुणनफल 1 प्राप्त करने के लिए, हमें `8/21` को निम्न से गुणा करना चाहिए –
`8/21`
`(-8)/21`
`21/8`
`(-21)/8`
– (–x) है –
– x
x
`1/x`
`(-1)/x`
`-1 1/7` का गुणन प्रतिलोम है –
`8/7`
`(-8)/7`
`7/8`
`7/(-8)`
यदि x कोई परिमेय संख्या है, तो x + 0 बराबर है –
x
0
– x
परिभाषित नहीं
1 का व्युत्क्रम है –
1
–1
0
परिभाषित नहीं
–1 का व्युत्क्रम है –
1
–1
0
परिभाषित नहीं
0 का व्युत्क्रम है –
1
–1
0
परिभाषित नहीं
किसी शून्येतर परिमेय संख्या `p/q` का व्युत्क्रम, जहाँ p और q पूर्णांक है और q ≠ 0 है, है –
`p/q`
1
0
`q/p`
यदि परिमेय संख्या x का व्युत्क्रम y है, तो y का व्युत्क्रम होगा –
x
y
`x/y`
`y/x`
`(-3)/8 xx ((-7)/13)` का व्युत्क्रम है –
`104/21`
`(-104)/21`
`21/104`
`(-21)/104`
निम्न में से कौन परिमेय संख्याओं के लिए, योग पर गुणन के वितरण गुण का उदाहरण है?
`-1/4 xx {2/3 + ((-4)/7)} = [-1/4 xx 2/3] + [-1/4xx((-4)/7)]`
`-1/4 xx {2/3 + ((-4)/7)} = [1/4 xx 2/3] - ((-4)/7)`
`-1/4 xx {2/3 + ((-4)/7)} = 2/3 + (-1/4) xx (-4)/7`
`-1/4 xx {2/3 + ((-4)/7)} = {2/3 + ((-4)/7)} - 1/4`
दी हुई परिमेय संख्याओं के बीच में, हम ज्ञात कर सकते है, ______।
एक और केवल एक परिमेय संख्या
केवल दो परिमेय संख्याएँ
केवल दस परिमेय संख्याएँ
अपरिमित रूप से अनेक
परिमेयसंख्याएँ
`(x + y)/2` एक परिमेय संख्या है जो, ______।
x और y के बीच में स्थित है
x और y दोनों से छोटी है
x और y दोनों से बड़ी है
x से छोटी परंतु y से बड़ी है
निम्न में से कौन-सा कथन सदैव सत्य है?
`(x - y)/2` परिमेय x और y संख्याओं के बीच एक परिमेय संख्या है
`(x + y)/2` परिमेय x और y संख्याओं के बीच एक परिमेय संख्या है
`(x xx y)/2` परिमेय x और y संख्याओं के बीच एक परिमेय संख्या है
`(x ÷ y)/2` परिमेय x और y संख्याओं के बीच एक परिमेय संख्या है
प्रश्न 26 से 47 में, रिक्त स्थानों को भरिए, ताकि कथन सत्य हो जाएँ -
`5/7` के तुल्य (समतुल्य) अंश 45 वाली परिमेय संख्या ______ है।
`7/9` के तुल्य हर 45 वाली परिमेय संख्या ______ हैं।
संख्या `15/20` और `35/40` में बड़ी संख्या ______ है।
एक धनात्मक परिमेय संख्या का व्युत्क्रम ______ होता है।
एक ऋणात्मक परिमेय संख्या का व्युत्क्रम ______ होता है।
शून्य का व्युत्क्रम ______ है।
संख्याएँ ______ और ______ स्वयं अपने व्युत्क्रम हैं।
यदि x का व्युत्क्रम y है, तो y2 का व्युत्क्रम x के पदों में ______ होगा।
`2/5 xx ((-4)/9)` का व्युत्क्रम ______ है।
(213 × 657)–1 = 213–1 × ______ है।
1 का ऋणात्मक ______ है।
परिमेय `a/b, c/d` और `e/f` संख्याओं के लिए, हमें `a/b xx (c/d + e/f)` = ______ + ______ प्राप्त है।
`(-5)/7, -3` से ______ है।
किन्ही दो परिमेय संख्याओं के बीच में ______ परिमेय संख्याएँ स्थित हैं।
संख्या रेखा पर परिमेय `1/3` और `(-1)/3` संख्याएँ शून्य के ______ ओर स्थित हैं।
एक ऋणात्मक परिमेय संख्या का ऋणात्मक सदैव एक ______ परिमेय संख्या होती है।
परिमेय संख्याओं को किसी भी ______ में जोड़ा या गुणा किया जा सकता है।
`(-5)/7` का व्युत्क्रम ______ है।
`4/3` का गुणन प्रतिलोम ______ है।
परिमेय संख्या 10.11, `p/q` के रूप में ______ है।
`1/5 xx [2/7 + 3/8] = [1/5 xx 2/7] +` ______ है।
–2 और –5 के बीच स्थित हर 1 वाली दो परिमेय संख्याएँ ______ और ______ है।
प्रश्न 48 से 99 में, बताइए कि कथन सत्य हैं या असत्य-
यदि `x/y` एक परिमेय संख्या है, तो y सदैव एक पूर्ण संख्या है।
सत्य
असत्य
यदि `p/q` एक परिमेय संख्या है, तो p शून्य के बराबर नहीं हो सकता।
सत्य
असत्य
यदि `r/s` एक परिमेय संख्या है, तो s शून्य के बराबर नहीं हो सकता।
सत्य
असत्य
`5/6, 2/3` और 1 संख्याओं के बीच स्थित है।
सत्य
असत्य
`5/10, 1/2` और 1 संख्याओं के बीच स्थित है।
सत्य
असत्य
`(-7)/2`, –3 और –4 संख्याओं के बीच स्थित है।
सत्य
असत्य
`9/6`, 1 और 2 संख्याओं के बीच स्थित है।
सत्य
असत्य
यदि a ≠ 0 है, तो `a/b` का गुणन प्रतिलोम `b/a` है।
सत्य
असत्य
`(-3)/5` का गुणन प्रतिलोम `5/3` है।
सत्य
असत्य
`1/2` का योज्य प्रतिलोम –2 है।
सत्य
असत्य
यदि `x/y, c/d` का योज्य प्रतिलोम है, तो `x/y + c/d = 0` है।
सत्य
असत्य
प्रत्येक परिमेय संख्या x के लिए, x + 1 = x होता है।
सत्य
असत्य
यदि `x/y, c/d` का योज्य प्रतिलोम है, तो `x/y - c/d = 0` है।
सत्य
असत्य
एक शून्येतर परिमेय संख्या `q/p` का व्युत्क्रम परिमेय संख्या `q/p` है।
सत्य
असत्य
यदि x + y = 0 है, तो –y, x का ऋणात्मक कहलाता है, जहाँ x और y परिमेय संख्याएँ है।
सत्य
असत्य
किसी परिमेय संख्या के ऋणात्मक का ऋणात्मक स्वयं वह संख्या ही होती है।
सत्य
असत्य
0 के ऋणात्मक का कोई अस्तित्व नहीं है।
सत्य
असत्य
1 का ऋणात्मक स्वयं 1 ही है।
सत्य
असत्य
सभी परिमेय x और y संख्याओं के लिए, x – y = y – x होता है।
सत्य
असत्य
सभी परिमेय संख्याओं x और y के लिए, x × y = y × x होता है।
सत्य
असत्य
सभी परिमेय संख्याओं x के लिए, x × 0 = x होता है।
सत्य
असत्य
सभी परिमेय संख्याओं x, y और z के लिए, x + (y × z) = (x + y) × (x + z) होता है।
सत्य
असत्य
सभी परिमेय संख्याओं a, b और c के लिए a(b + c) = ab + bc होता है।
सत्य
असत्य
केवल 1 ही ऐसी परिमेय संख्या है, जो स्वयं अपना व्युत्क्रम है।
सत्य
असत्य
–1 किसी भी परिमेय संख्या का व्युत्क्रम नहीं है।
सत्य
असत्य
किसी भी परिमेय संख्या x के लिए, x + (–1) = –x है।
सत्य
असत्य
दो परिमेय संख्याओं x और y में, यदि x < y है, तो x – y एक धनात्मक परिमेय संख्या है।
सत्य
असत्य
यदि x और y ऋणात्मक परिमेय संख्याएँ हैं, तो x + y भी एक ऋणात्मक परिमेय संख्या होती है।
सत्य
असत्य
किन्हीं दो परिमेय संख्याओं के बीच में ठीक दस परिमेय संख्याएँ स्थित होती है।
सत्य
असत्य
परिमेय संख्याएँ योग और गुणन के अंतर्गत संवृत हैं, परंतु व्यवकलन के अंतर्गत संवृत नहीं है।
सत्य
असत्य
परिमेय संख्याओं का व्यवकलन क्रम विनिमेय है।
सत्य
असत्य
`-3/4, -2` से छोटी है।
सत्य
असत्य
0 एक परिमेय संख्या है।
सत्य
असत्य
सभी घनात्मक परिमेय संख्याएँ 0 और 1000 के बीच स्थित हैं।
सत्य
असत्य
वर्ष 2004 - 05 की भारत की जनसंख्या एक परिमेय संख्या है।
सत्य
असत्य
`5/6` और `8/9` के बीच अनगिनत परिमेय संख्याएँ है।
सत्य
असत्य
x–1 का व्युत्क्रम `1/x` है।
सत्य
असत्य
संख्या रेखा पर, परिमेय संख्या `57/23` शून्य के बायीं ओर स्थित है।
सत्य
असत्य
संख्या रेखा पर, परिमेय संख्या `7/(-4)` शून्य के दायीं ओर स्थित है।
सत्य
असत्य
संख्या रेखा पर, परिमेय संख्या `(-8)/(-3)` शून्य के बायीं ओर स्थित है।
सत्य
असत्य
परिमेय `1/2` और –1 संख्याएँ संख्या रेखा पर शून्य के विपरीत ओर स्थित हैं।
सत्य
असत्य
प्रत्येक भिन्न एक परिमेय संख्या है।
सत्य
असत्य
प्रत्येक पूर्णांक एक परिमेय संख्या है।
सत्य
असत्य
परिमेय संख्याओं को संख्या रेखा पर निरूपित किया जा सकता है।
सत्य
असत्य
एक ऋणात्मक परिमेय संख्या का ऋणात्मक एक धनात्मक परिमेय संख्या होती है।
सत्य
असत्य
यदि x और y ऐसी दो परिमेय संख्याएँ हैं कि x > y है, तो x – y सदैव एक धनात्मक परिमेय संख्या है।
सत्य
असत्य
0 सबसे छोटी परिमेय संख्या है।
सत्य
असत्य
प्रत्येक पूर्ण संख्या एक पूर्णांक है।
सत्य
असत्य
प्रत्येक पूर्ण संख्या एक परिमेय संख्या है।
सत्य
असत्य
0 एक पूर्ण संख्या है परंतु यह एक परिमेय संख्या नहीं है।
सत्य
असत्य
परिमेय संख्याएँ `1/2` और `-5/2` संख्या रेखा पर शून्य के विपरीत और स्थित हैं।
सत्य
असत्य
परिमेय संख्याओं को किसी भी क्रम में जोड़ा (या गुणा) किया जा सकता है।
`(-4)/5 xx (-6)/5 = (-6)/5 xx (-4)/5`
सत्य
असत्य
वे परिमेय संख्याएँ चुनिए जो पूर्णांक भी हैं :
`9/4, 8/4, 7/4, 6/4, 9/3, 8/3, 7/3, 6/3, 5/2, 4/2, 3/1, 3/2, 1/1, 0/1, (-1)/1, (-2)/1, (-3)/2, (-4)/2, (-5)/2, (-6)/2`
वे परिमेय संख्याएँ चुनिए जिन्हें उनके न्यूनतम रूप में हर 4 वाली परिमेय संख्या के रूप में लिखा जा सकता है –
`7/8, 64/16, 36/(-12), (-16)/17, 5/(-4), 140/28`
उपयुक्त पुनर्व्यस्थितिकरण द्वारा योग ज्ञात कीजिए –
`4/7 + ((-4)/9) + 3/7 + ((-13)/9)`
उपयुक्त पुनर्व्यस्थितिकरण द्वारा योग ज्ञात कीजिए –
`-5 + 7/10 + 3/7 + (-3) + 5/14 + (-4)/5`
निम्न के लिए – (– x) = x को सत्यापित कीजिए –
x = `3/5`
निम्न के लिए – (– x) = x को सत्यापित कीजिए –
x = `(-7)/9`
निम्न के लिए – (– x) = x को सत्यापित कीजिए –
x = `13/(-15)`
यह दर्शाने के लिए कि परिमेय संख्याएँ योग, व्यवकलन और गुणन के लिए संवृत्त है एक-एक उदाहरण दीजिए। क्या परिमेय संख्याएँ विभाजन के अंतर्गत संवृत्त हैं? अपने उत्तर की पुष्टि के लिए दो उदाहरण दीजिए।
निम्न को लेकर परिमेय संख्याओं के गुण x + y = y + x का सत्यापन कीजिए –
`x = 1/2, y = 1/2`
निम्न को लेकर परिमेय संख्याओं के गुण x + y = y + x का सत्यापन कीजिए –
`x = (-2)/3, y = (-5)/6`
निम्न को लेकर परिमेय संख्याओं के गुण x + y = y + x का सत्यापन कीजिए –
`x = (-3)/7, y = 20/21`
निम्न को लेकर परिमेय संख्याओं के गुण x + y = y + x का सत्यापन कीजिए –
`x = (-2)/5, y = (-9)/10`
निम्न में से प्रत्येक को उपयुक्त गुण का प्रयोग करते हुए सरल कीजिए। साथ ही, उस गुण का नाम भी लिखिए –
`[1/2 xx 1/4] + [1/2 xx 6]`
निम्न में से प्रत्येक को उपयुक्त गुण का प्रयोग करते हुए सरल कीजिए। साथ ही, उस गुण का नाम भी लिखिए –
`[1/5 xx 2/15] - [1/5 xx 2/5]`
निम्न में से प्रत्येक को उपयुक्त गुण का प्रयोग करते हुए सरल कीजिए। साथ ही, उस गुण का नाम भी लिखिए –
`(-3)/5 xx {3/7 + ((-5)/6)}`
बताइए कि किस गुण द्वारा आप `1/5 xx [5/6 xx 7/9]` को `[1/5 xx 5/6] xx 7/9` के रूप में लिखकर अभिकलित कर सकते है।
निम्न को लेकर परिमेय संख्याओं के गुण x × y = y × x का सत्यापन कीजिए –
`x = 7` और `y = 1/2`
निम्न को लेकर परिमेय संख्याओं के गुण x × y = y × x का सत्यापन कीजिए –
`x = 2/3` और `y = 9/4`
निम्न को लेकर परिमेय संख्याओं के गुण x × y = y × x का सत्यापन कीजिए –
`x = (-5)/7` और `y = 14/15`
निम्न को लेकर परिमेय संख्याओं के गुण x × y = y × x का सत्यापन कीजिए –
`x = (-3)/8` और `y = (-4)/9`
निम्न का प्रयोग करते हुए, परिमेय संख्याओं के गुण x × (y × z) = (x × y) × z का सत्यापन कीजिए –
`x = 1, y = (-1)/2` और `z = 1/4`
इस गुण का नाम क्या है?
निम्न का प्रयोग करते हुए, परिमेय संख्याओं के गुण x × (y × z) = (x × y) × z का सत्यापन कीजिए –
`x = 2/3, y = (-3)/7` और `z = 1/2`
इस गुण का नाम क्या है?
निम्न का प्रयोग करते हुए, परिमेय संख्याओं के गुण x × (y × z) = (x × y) × z का सत्यापन कीजिए –
`x = (-2)/7, y = (-5)/6` और `z = 1/4`
इस गुण का नाम क्या है?
निम्न का प्रयोग करते हुए, परिमेय संख्याओं के गुण x × (y × z) = (x × y) × z का सत्यापन कीजिए –
`x = 0, y = 1/2` और `z = 1/4`
इस गुण का नाम क्या है?
निम्न को लेकर, परिमेय संख्याओं के गुण x × (y + z) = x × y + x × z का सत्यापन कीजिए –
`x = (-1)/2, y = 3/4, z = 1/4`
निम्न को लेकर, परिमेय संख्याओं के गुण x × (y + z) = x × y + x × z का सत्यापन कीजिए –
`x = (-1)/2, y = 2/3, z = 3/4`
निम्न को लेकर, परिमेय संख्याओं के गुण x × (y + z) = x × y + x × z का सत्यापन कीजिए –
`x = (-2)/3, y = (-4)/6, z = (-7)/9`
निम्न को लेकर, परिमेय संख्याओं के गुण x × (y + z) = x × y + x × z का सत्यापन कीजिए –
`x = (-1)/5, y = 2/15, z = (-3)/10`
परिमेय संख्याओं के योग पर गुणन के वितरण गुण का प्रयोग करते हुए, सरल कीजिए –
`3/5 xx [35/24 + 10/1]`
परिमेय संख्याओं के योग पर गुणन के वितरण गुण का प्रयोग करते हुए, सरल कीजिए –
`(-5)/4 xx [8/5 + 16/15]`
परिमेय संख्याओं के योग पर गुणन के वितरण गुण का प्रयोग करते हुए, सरल कीजिए –
`2/7 xx [7/16 - 21/4]`
परिमेय संख्याओं के योग पर गुणन के वितरण गुण का प्रयोग करते हुए, सरल कीजिए –
`3/4 xx [8/9 - 40]`
सरल कीजिए –
`32/5 + 23/11 xx 22/15`
सरल कीजिए –
`3/7 xx 28/15 ÷ 14/5`
सरल कीजिए –
`3/7 + (-2)/21 xx (-5)/6`
सरल कीजिए –
`7/8 + 1/16 - 1/12`
निम्न में वह परिमेय संख्या पहचानिए, जो अन्य तीन संख्याओं से भिन्न प्रकार की है। अपने कारण को स्पष्ट कीजिए।
`(-5)/11, (-1)/2, (-4)/9, (-7)/3`
`19/4` मीटर तार का मूल्य ₹ `171/2` है। एक मीटर तार का मूल्य ज्ञात कीजिए।
एक रेलगाड़ी `17/2` घंटों में `1445/2` किलोमीटर की दूरी तय करती है। उस रेलगाड़ी की किलोमीटर/घंटा में चाल ज्ञात कीजिए।
यदि समान साइज की 16 कमीज 24 m कपड़े से बनायी जा सकती हैं, तो एक कमीज को बनाने के लिए कितने कपड़े की आवश्यकता होगी?
हामिद के खाते की कुल जमा धनराशि का `7/11` भाग ₹ 77,000 के बराबर है। हामिद के खाते में कितनी धनराशि जमा है?
`117 1/3` m लंबी एक रस्सी को `7 1/3` m लंबे बराबर टुकड़ों में काटा जाता है। इसमें ऐसे कितने टुकड़े होंगे?
एक कक्षा के विद्यार्थियों की संख्या में से `1/6` औसत से ऊपर हैं, `1/4` औसत हैं तथा शेष विद्यार्थी औसत से नीचे हैं। यदि विद्यार्थियों की कुल संख्या 48 है तो कक्षा में कितने विद्यार्थी औसत से नीचे हैं?
किसी स्कूल के कुल विद्यार्थियों में से `2/5` विद्यार्थी कार से स्कूल आते हैं, जबकि `1/4` विद्यार्थी बस से स्कूल आते हैं। अन्य विद्यार्थी स्कूल पैदल आते हैं, जिनमें से `1/3` स्वयं पैदल चल कर आते हैं तथा शेष अपने माता-पिता के साथ पैदल चल कर आते हैं। यदि 224 विद्यार्थी स्वयं पैदल चल कर स्कूल आते हैं, तो उस स्कूल में कुल कितने विद्यार्थी हैं?
हुमा, हुब्ना और सीमा को अपनी माँ से ₹ 2,016 की कुल धनराशि मासिक भत्ते के रूप में इस प्रकार मिलती है कि सीमा को हुमा की धनराशि के `1/2` के बराबर की धनराशि मिलती है तथा हुब्ना को सीमा की धनराशि से `1 2/3` गुनी धनराशि मिलती है। इन तीनों बहनों को पृथक-पृथक कितनी धनराशि मिलती है?
एक माँ और उसकी दो पुत्रियों ने एक कमरे का निर्माण ₹ 62,000 में करवाया। बड़ी पुत्री ने अपनी माँ के भाग की धनराशि की `3/8` धनराशि का योगदान दिया तथा छोटी पुत्री ने अपनी माँ के भाग की धनराशि की `1/2` धनराशि दी। तीनों ने पृथक-पृथक कितनी धनराशि का योगदान दिया?
बताइए कि किन गुणों द्वारा आप `2/3 xx [3/4 xx 5/7]` और `[2/3 xx 5/7] xx 3/4` की तुलना कर सकते हैं।
निम्न में प्रयोग किए गुण का नाम बताइए :
`-7/11 xx (-3)/5 = (-3)/5 xx (-7)/11`
निम्न में प्रयोग किए गुण का नाम बताइए :
`-2/3 xx [3/4 + (-1)/2] = [(-2)/3 xx 3/4] + [(-2)/3 xx (-1)/2]`
निम्न में प्रयोग किए गुण का नाम बताइए :
`1/3 + [4/9 + ((-4)/3)] = [1/3 + 4/9] + [(-4)/3]`
निम्न में प्रयोग किए गुण का नाम बताइए :
`(-2)/7 + 0 = 0 + (-2)/7 = - 2/7`
निम्न में प्रयोग किए गुण का नाम बताइए :
`3/8 xx 1 = 1 xx 3/8 = 3/8`
निम्न का गुणन प्रतिलोम ज्ञात कीजिए –
`-1 1/8`
निम्न का गुणन प्रतिलोम ज्ञात कीजिए –
`3 1/3`
संख्या `1/4, 13/16, 5/8 ` को अवरोही क्रम में व्यवस्थित कीजिए।
दो परिमेय संख्याओं का गुणनफल `(-14)/27` है। यदि इनमें से एक संख्या `7/9` है, तो दूसरी संख्या ज्ञात कीजिए।
`(-15)/20` को हम किस संख्या से गुणा करें ताकि गुणनफल `(-5)/7` प्राप्त हो ?
`(-8)/13` को हम किस संख्या से गुणा करें ताकि गुणनफल 24 प्राप्त हो?
दो परिमेय संख्याओं का गुणन –7 है। यदि इनमें से एक संख्या –5 है, तो दूसरी संख्या ज्ञात कीजिए।
क्या आप कोई ऐसी संख्या ज्ञात कर सकते हैं जिसका गुणन प्रतिलोम –1 है? यदि हाँ, तो उसे ज्ञात कीजिए।
0 और 1 के बीच पाँच परिमेय संख्याएँ ज्ञात कीजिए।
दो परिमेय ज्ञात कीजिए, जिनका निरपेक्ष (संख्यात्मक) मान `1/5` हैं।
40 मीटर लंबी एक रस्सी में से बराबर के टुकड़े काटे जाते हैं। यदि एक टुकड़े की लंबाई `10/3` मीटर है, तो ऐसे टुकड़ों की संख्या ज्ञात कीजिए।
`5 1/2` मीटर लंबी एक रस्सी को 12 बराबर टुकड़ों में काटा जाता है। प्रत्येक टुकड़े की लंबाई क्या है?
निम्न परिमेय संख्याओं को अवरोही क्रम में व्यवस्थित कीजिए –
`8/7, (-9)/8, (-3)/2, 0, 2/5`
ज्ञात कीजिए –
`0 ÷ 2/3`
ज्ञात कीजिए –
`1/3 xx (-5)/7 xx (-21)/10`
हिमाचल प्रदेश के एक स्थान का सर्दियों में एक दिन का तापमान –16°C था। सूत्र `C/5 = (F - 32)/9` का प्रयोग करते हुए, इस तापमान को डिग्री फॉरेनहाइट (°F) में बदलिए।
7 के योज्य प्रतिलोम और गुणन प्रतिलोम का योग ज्ञात कीजिए।
`-1/3` के योज्य प्रतिलोम ओर गुणन प्रतिलोम का गुणनफल ज्ञात कीजिए।
नीचे दिए हुए आरेख में चिड़ियों की विभिन्न प्रजातियों के पंखों के उत्तर देने के लिए, इस आरेख का प्रयोग कीजिए –
| अल्बाट्रोस | समुद्री गुल |
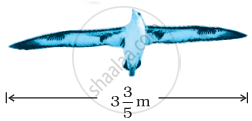 |
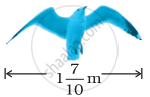 |
एक समुद्री गुल के पंखों से एक अल्बाट्रोस के पंख कितने अधिक लंबे हैं?
नीचे दिए हुए आरेख में चिड़ियों की विभिन्न प्रजातियों के पंखों के उत्तर देने के लिए, इस आरेख का प्रयोग कीजिए –
| गोल्डन ईगल | ब्लू जय |
 |
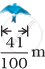 |
एक ब्लू जय के पंखों से एक गोल्डन ईगल के पंख कितने अधिक लंबे है?
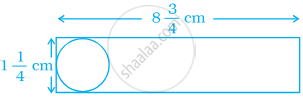
एक एल्युमिनियम की विमाओं `8 3/4` cm × `1 1/4` cm की पट्टी में से शालिनी को ` 1 1/4` cm व्यास वाले वृत्त काटने है। शालिनी कितने पुरे वृत्त काट सकती है? साथ ही, इसमें नष्ट हुई एल्युमिनियम की पट्टी भी परिकलित कीजिए।
फलों के एक सलाद की रेसिपी (recipe) के लिए `1/2` कप चीनी की आवश्यकता है। फलों के इसी सलाद की एक अन्य रेसिपी के लिए, दो बड़े चम्मच चीनी की आवश्यकता है। यदि 1 बड़ा चम्मच `1/16` कप के समतुल्य है, तो पहली रेसिपी को कितनी अधिक चीनी की आवश्यकता है?
चार मित्रों में यह देखने के लिए की एक पंजे पर कौन कितनी दूर उछल कर चल पाता है, एक प्रतियोगिता आयोजित की। उनके द्वारा तय की गयी दूरियाँ नीचे सारणी में दी गई है –
| नाम | तय की गई दूरी (किमी.) |
| सीमा | `1/25` |
| नैन्सी | `1/32` |
| मेघा | `1/40` |
| सोनी | `1/20` |
- सोनी नैन्सी से कितनी अधिक दूर चल पाती है?
- सीमा और मेघा द्वारा तय की गयी कुल दूरी कितनी हैं?
- कौन अधिक दूर चली-नैन्सी या मेघा?
नीचे दी हुई सारणी में किसी राज्य के चार गाँवों की किलोमीटर में दूरियाँ प्रदर्शित की गयी हैं। दो गाँवों के बीच की दूरी ज्ञात करने के लिए, वह वर्ग निर्धारित कीजिए जहाँ एक गाँव की पंक्ति दूसरे गाँव के स्तंभ से प्रतिच्छेद करती है।
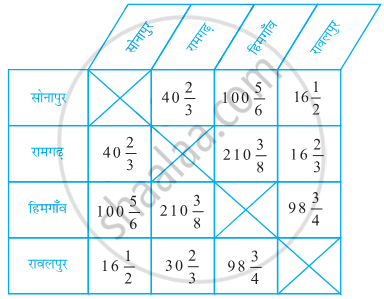
हिमगाँव और रावलपुर के बीच की दुरी की सोनापुर और रामगढ़ के बीच की दुरी से तुलना कीजिए।
नीचे दी हुई सारणी में किसी राज्य के चार गाँवों की किलोमीटर में दूरियाँ प्रदर्शित की गयी हैं। दो गाँवों के बीच की दूरी ज्ञात करने के लिए, वह वर्ग निर्धारित कीजिए जहाँ एक गाँव की पंक्ति दूसरे गाँव के स्तंभ से प्रतिच्छेद करती है।
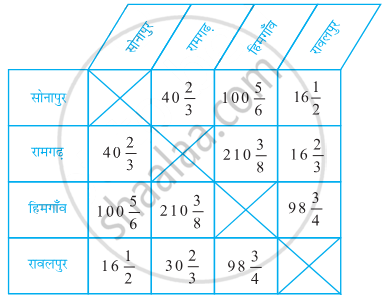
यदि आप हिमगाँव से सोनापुर गाड़ी चलाते हुए जाएँ और फिर सोनापुर से रावलपुर जाएँ, तो आपने कितनी दूर गाड़ी चला ली होगी?
नीचे दी हुई सारणी कुछ सामान्य पदार्थों के उन भागों को प्रदर्शित करती है, जो पुनः प्रयुक्त किये जाते है –
| पदार्थ | पुनः प्रयुक्त |
| कागज | `5/11` |
| एल्युमिनियम के डिब्बे | `5/8` |
| काँच | `2/5` |
| अन्य | `3/4` |
- क्या कागज को पुनः प्रयुक्त व्यक्त करने वाली परिमेय संख्या `1/2` से अधिक है या `1/2` से छोटी है?
- किन पदार्थों की पुनः प्रयुक्त मात्रा `1/2` से कम है?
- एल्युमिनियम के डिब्बों की पुनः प्रयुक्त मात्रा एल्युमिनियम के डिब्बों की मात्रा के आधे से अधिक है या कम है?
- बड़े से छोटे क्रम में पुनः प्रयुक्त मात्राओं को व्यवस्थित कीजिए।
कई चौड़े स्क्रीन वाले टेलीविजनों की सेंटीमीटरों में सामान्य चौड़ाइयाँ `98 4/9, 98 1/25`और 97.94 हैं। इन संख्याओं को `p/q` के रूप की परिमेय संख्याओं के रूप में व्यक्त कीजिए तथा चौड़ाइयों को आरोही क्रम में व्यवस्थित कीजिए।
किसी मनोरंजन पार्क में बना रोलर कोस्टर `2/3` m ऊँचा है। यदि इस पार्क में एक नया रोलर कोस्टर बनाया जाये, जिसकी ऊँचाई वर्तमान कोस्टर की ऊँचाई की `3/5` गुनी हो तो नये रोलर कोस्टर की ऊँचाई क्या होगी?
नीचे दी हुई सारणी किसी शहर में कुछ महीनों में हुई कुल वर्षा की औसत मासिक वर्षा से की गयी तुलना से सबंधित सूचना को दर्शाती है। प्रत्येक दशमलव को `p/q` के रूप की परिमेय संख्या के रूप में लिखिए।
| महीना | सामान्य (cm में) से ऊपर/नीचे |
| मई | 2.6924 |
| जून | 0.6096 |
| जुलाई | – 6.9088 |
| अगस्त | – 8.636 |
कुछ राज्यों में पुरुषों के जीवन काल की औसत प्रत्याशाएँ नीचे सारणी में दर्शायी गई है। प्रत्येक दशमलव को `p/q` के रूप में व्यक्त कीजिए तथा राज्यों को सबसे कम से सबसे अधिक पुरुष जीवन काल प्रत्याशाओं के क्रम में व्यवस्थित कीजिए। राज्य अनुसार आंकड़े नीचे दिए हैं ; प्रत्येक राज्य के लिए होमपेज के "FACTFILE" खंड में अधिक सूचक ज्ञात किए जा सकते है।
| राज्य | पुरुष | `bb(p/q)` रूप | न्यूनतम रूप |
| आंध्र प्रदेश | 61.6 | ||
| असम | 57.1 | ||
| बिहार | 60.7 | ||
| गुजरात | 61.9 | ||
| हरियाणा | 64.1 | ||
| हिमाचल प्रदेश | 65.1 | ||
| कर्नाटक | 62.4 | ||
| केरल | 70.6 | ||
| मध्य प्रदेश | 56.5 | ||
| महाराष्ट्र | 64.5 | ||
| ओडिशा | 57.6 | ||
| पंजाब | 66.9 | ||
| राजस्थान | 59.8 | ||
| तमिलनाडु | 63.7 | ||
| उत्तर प्रदेश | 58.9 | ||
| पश्चिम बंगाल | 62.8 | ||
| भारत | 60.8 |
स्त्रोत ; रजिस्ट्रार जनरल ऑफ़ इंडिया (2003) की एस आर एस पर आधारित संक्षिप्त की गई सारणियाँ। एस आर एस वैश्लेषिक अध्ययन, 2003 की रिपोर्ट 3 : रजिस्ट्रार जनरल ऑफ़ इंडिया, नई दिल्ली। यह आँकड़े समय अवधि 1995 – 99 के है। बाद में, राज्य विभाजित हो गए थे, परंतु केवल वे ही इस रिपोर्ट में सम्मलित है जो विभाजन से पूर्व थे। (मध्य प्रदेश में छत्तीसगढ़, यूपी में उत्तरखंड और बिहार में झारखंड)
एक स्कर्ट, जो `35 7/8` cm लंबी है, मैं `3 1/8` cm किनारी लगी हुई है। यदि किनारी को हटा दिया जाए, तो स्कर्ट की लंबाई कितनी हो जाएगी?
मानवी और कुबेर में से प्रत्येक को बराबर भत्ता मिलता है। निचे दी गयी सारणी यह प्रदर्शित करती है की वे अपने बचत खाते में अपने भत्ते की कितनी भिन्न (या भाग) जमा करते हैं तथा साथ ही वह भिन्न (या भाग) जो वे मॉल जाकर व्यय करते हैं। यदि प्रत्येक का भत्ता 1260 ₹ है, तो प्रत्येक की शेष राशि ज्ञात कीजिए।
| धनराशि कहाँ जाती है | भत्ते की भिन्न (का भाग) | |
| मानवी | कुबेर | |
| बचत खाता | `1/2` | `1/3` |
| माल पर व्यय | `1/4` | `3/5` |
| बची हुई राशि | ? | ? |
Solutions for 1: परिमेय संख्याएँ
![NCERT Exemplar solutions for Mathematics [Hindi] Class 8 chapter 1 - परिमेय संख्याएँ NCERT Exemplar solutions for Mathematics [Hindi] Class 8 chapter 1 - परिमेय संख्याएँ - Shaalaa.com](/images/mathematics-hindi-class-8_6:5f2b1b2038084cf381bfa42c826a928c.jpg)
NCERT Exemplar solutions for Mathematics [Hindi] Class 8 chapter 1 - परिमेय संख्याएँ
Shaalaa.com has the CBSE Mathematics Mathematics [Hindi] Class 8 CBSE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. NCERT Exemplar solutions for Mathematics Mathematics [Hindi] Class 8 CBSE 1 (परिमेय संख्याएँ) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. NCERT Exemplar textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [Hindi] Class 8 chapter 1 परिमेय संख्याएँ are दो परिमेय संख्याओं के बीच में परिमेय संख्याएँ, परिमेय संख्याएँ, परिमेय संख्याओं के गुणधर्म, परिमेय संख्याओं का संवृत गुणधर्म, परिमेय संख्याओं का क्रमविनिमेयता गुणधर्म, परिमेय संख्याओं का साहचर्यता (सहचारिता) गुणधर्म, परिमेय संख्याओं के लिए गुणन की योग पर वितरकता, परिमेय संख्याओं का योज्य तत्समक तथा गुणात्मक तत्समक गुणधर्म, परिमेय संख्याओं का ऋणात्मक अथवा योज्य प्रतिलोम, परिमेय संख्याओं का व्युत्क्रम अथवा गुणात्मक प्रतिलोम, परिमेय संख्याओं का संख्या रेखा पर निरूपण.
Using NCERT Exemplar Mathematics [Hindi] Class 8 solutions परिमेय संख्याएँ exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in NCERT Exemplar Solutions are essential questions that can be asked in the final exam. Maximum CBSE Mathematics [Hindi] Class 8 students prefer NCERT Exemplar Textbook Solutions to score more in exams.
Get the free view of Chapter 1, परिमेय संख्याएँ Mathematics [Hindi] Class 8 additional questions for Mathematics Mathematics [Hindi] Class 8 CBSE, and you can use Shaalaa.com to keep it handy for your exam preparation.
