Advertisements
Advertisements
Question
Let R be set of points inside a rectangle of sides a and b (a, b > 1) with two sides along the positive direction of x-axis and y-axis. Then ______.
Options
R = {(x, y) : 0 ≤ x ≤ a, 0 ≤ y ≤ b}
R = {(x, y) : 0 ≤ x < a, 0 ≤ y ≤ b}
R = {(x, y) : 0 ≤ x ≤ a, 0 < y < b}
R = {(x, y) : 0 < x < a, 0 < y < b}
Solution
Let R be set of points inside a rectangle of sides a and b (a, b > 1) with two sides along the positive direction of x-axis and y-axis. Then R = {(x, y) : 0 < x < a, 0 < y < b}.
Explanation:
Let OABC be a rectangle whose sides a and b are along the positive direction of X and Y respectively.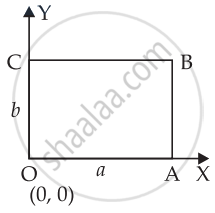
∴ Clearly, R = {(x, y) : 0 < x < a and 0 < y < b}
APPEARS IN
RELATED QUESTIONS
Identify whether the following is set or not? Justify your answer.
A team of eleven best-cricket batsmen of the world.
Identify whether the following is set or not? Justify your answer.
The collection of all even integers.
List all the elements of the following set:
E = {x : x is a month of a year not having 31 days}
List all the elements of the following set:
F = {x : x is a consonant in the English alphabet which precedes k}.
Which of the following collection are sets? Justify your answer:
The collection of difficult topics in mathematics.
If A = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], then insert the appropriate symbol ∈ or ∉ in each of the following blank space:
−2 ...... A
Describe the following sets in Roster form:
The set of all letters in the word 'Better'.
Describe the following sets in set-builder form:
B={1,1/2 ,1/3, 1/4,1/5,...........};
Which of the following statement are correct?
Write a correct form of each of the incorrect statement.
\[\left\{ b, c \right\} \subset \left\{ a, \left\{ b, c \right\} \right\}\]
Which of the following statement are correct?
Write a correct form of each of the incorrect statement.
\[\left\{ a, b \right\} \subset \left\{ a, \left\{ b, c \right\} \right\}\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[1 \in A\]
Let\[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true?
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true? \[\left\{ 1 \right\} \in A\]
Write down all possible proper subsets each of the following set:
{1, 2},
Write down all possible proper subsets each of the following set:
{1}.
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
2 _____ A
Describe the following set in Set-Builder form
{0}
If A = {x/6x2 + x – 15 = 0}, B = {x/2x2 – 5x – 3 = 0}, C = {x/2x2 – x – 3 = 0} then find (A ∩ B ∩ C)
Write the following sets in the roaster form.
A = {x | x is a positive integer less than 10 and 2x – 1 is an odd number}
Write the following sets in the roaster form.
C = {x : x2 + 7x – 8 = 0, x ∈ R}
Write the following sets in the roaster form:
D = {t | t3 = t, t ∈ R}
State which of the following statements is true and which is false. Justify your answer.
496 ∉ {y | the sum of all the positive factors of y is 2y}.
Determine whether the following statement is true or false. Justify your answer.
For all sets A, B, and C, A – (B – C) = (A – B) – C
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in more than one subject only
In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Find the number of students who play neither?
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study French only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study French and English but not Sanskrit
The set {x ∈ R : 1 ≤ x < 2} can be written as ______.
