Advertisements
Advertisements
Question
Let S = set of points inside the square, T = the set of points inside the triangle and C = the set of points inside the circle. If the triangle and circle intersect each other and are contained in a square. Then ______.
Options
S ∩ T ∩ C = Φ
S ∪ T ∪ C = C
S ∪ T ∪ C = S
S ∪ T = S ∩ C
Solution
Let S = set of points inside the square, T = the set of points inside the triangle and C = the set of points inside the circle. If the triangle and circle intersect each other and are contained in a square. Then S ∪ T ∪ C = S.
Explanation:
The given conditions of the question may be represented by the following Venn diagram.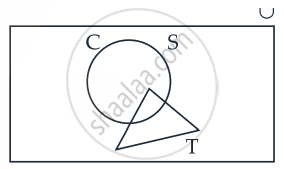
From the given Venn diagram, we clearly conclude that S ∪ T ∪ C = S
APPEARS IN
RELATED QUESTIONS
Identify whether the following is set or not? Justify your answer.
The collection of all even integers.
Write the following set in roster form:
D = {x : x is a prime number which is divisor of 60}
Write the following set in the set-builder form:
{2, 4, 8, 16, 32}
Which of the following collection is set? Justify your answer:
The collection of ten most talented writers of India.
Which of the following collection are sets? Justify your answer:
The collection of difficult topics in mathematics.
Which of the following collection are sets? Justify your answer:
A collection of novels written by Munshi Prem Chand.
If A = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], then insert the appropriate symbol ∈ or ∉ in each of the following blank space:
−2 ...... A
Describe the following set in Roster form:
The set of all letters in the word 'Trigonometry'
Describe the following sets in set-builder form:
{1, 4, 9, 16, ..., 100}
Describe the following sets in set-builder form:
{2, 4, 6, 8 .....}
List all the elements of the following sets:
\[A = \left\{ x: x^2 \leq 10, x \in Z \right\}\]
Write the set of all vowels in the English alphabet which precede q.
Which of the following statement are correct?
Write a correct form of each of the incorrect statements.
\[a \subset \left\{ a, b, c \right\}\]
Which of the following statemen are correct?
Write a correct form of each of the incorrect statement.
\[\left\{ a, b \right\} \subset \left\{ a, \left\{ b, c \right\} \right\}\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\phi \in A\]
Write down all possible subsets of each of the following set:
{a}
Describe the following set in Roster form
A = {x/x is a letter of the word 'MOVEMENT'}
Select the correct answer from given alternative.
In a city 20% of the population travels by car, 50% travels by bus and 10% travels by both car and bus. Then, persons travelling by car or bus are
Write the following sets in the roaster form.
C = {x : x2 + 7x – 8 = 0, x ∈ R}
Write the following sets in the roaster form:
D = {t | t3 = t, t ∈ R}
If Y = {x | x is a positive factor of the number 2p – 1 (2p – 1), where 2p – 1 is a prime number}.Write Y in the roaster form.
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in Mathematics only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study Sanskrit only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study none of the three languages
In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Then, the number of students who play neither is ______.
The set {x ∈ R : 1 ≤ x < 2} can be written as ______.
