Advertisements
Advertisements
Question
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in Mathematics only
Solution
Let the number of students passed in Mathematics M, E be in English and S be in Science.
Then n(U) = 100
n(M) = 12
n(E) = 15
n(S) = 8
n(E ∩ M) = 6
n(M ∩ S) = 7
n(E ∩ S) = 4
And n(E ∩ M ∩ S) = 4
Let us draw a Venn diagram.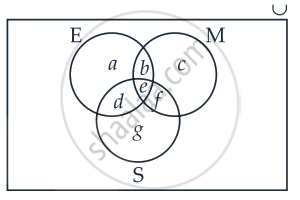
According to the Venn diagram, we get
a + b + d + e = 15 ......(i)
b + c + e + f = 12 ......(ii)
d + e + f + g = 8 .....(iii)
n(E ∩ M) = 6
∴ b + e = 6 ......(iv)
n(M ∩ S) = 7
∴ e + f = 7 ......(v)
n(E ∩ S) = 4
∴ d + e = 4 ......(vi)
And n(E ∩ M ∩ S) = 4
∴ e = 4 ......(vii)
From equation (iv) and (vii)
We get b + 4 = 6
∴ b = 2
From equation (v) and (vii)
We get 4 + f = 7
∴ f = 3
From equation (vi) and (vii)
We get d + 4 = 4
∴ d = 0
From equation (i) we get
a + b + d + e = 15
⇒ a + 2 + 0 + 4 = 15
⇒ a = 9
From equation (ii)
b + c + e + f = 12
⇒ 2 + c + 4 + 3 = 12
⇒ c = 3
From equation (iii)
d + e + f + g = 8
⇒ 0 + 4 + 3 + g = 8
⇒ g = 1
∴ Number of students who passed in Mathematics only, c = 3.
APPEARS IN
RELATED QUESTIONS
Write the following set in roster form:
C = {x : x is a two-digit natural number such that the sum of its digits is 8}
Write the following set in roster form:
E = The set of all letters in the word TRIGONOMETRY
List all the elements of the following set:
A = {x : x is an odd natural number}
Which of the following collection are sets? Justify your answer:
A collection of novels written by Munshi Prem Chand.
Describe the following sets in Roster form:
{x ∈ N : x2 < 25};
Describe the following sets in Roster form:
The set of all letters in the word 'Better'.
Describe the following sets in set-builder form:
D = {10, 11, 12, 13, 14, 15};
List all the elements of the following sets:
\[A = \left\{ x: x^2 \leq 10, x \in Z \right\}\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[a \in A\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\phi \in A\]
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\]Which of the following are true? \[\left\{ 1 \right\} \in A\]
Let \[\left\{ \left\{ 2 \right\}, \left\{ 1 \right\} \right\} \not\subset A\] Which of the following are true? \[\left\{ \left\{ 2 \right\}, \left\{ 1 \right\} \right\} \not\subset A\]
Write down all possible subsets of each of the following set:
{a}
Write down all possible subsets of each of the following set:
{0, 1},
Write down all possible subsets of each of the following set:
{a, b, c},
Write down all possible proper subsets each of the following set:
{1, 2},
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
4 _____ A
Describe the following set in Set-Builder form
{0, ±1, ±2, ±3}
From amongst 2000 literate individuals of a town, 70% read Marathi newspapers, 50% read English newspapers and 32.5% read both Marathi and English newspapers. Find the number of individuals who read neither Marathi and English newspaper
There are 260 persons with skin disorders. If 150 had been exposed to chemical A, 74 to chemical B, and 36 to both chemicals A and B, find the number of persons exposed to Chemical B but not Chemical A
Write the following interval in Set-Builder form
`(6, ∞)`
Write the following sets in the roaster from:
A = {x : x ∈ R, 2x + 11 = 15}
Write the following sets in the roaster form:
F = {x | x4 – 5x2 + 6 = 0, x ∈ R}
State which of the following statements is true and which is false. Justify your answer.
496 ∉ {y | the sum of all the positive factors of y is 2y}.
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in English and Mathematics but not in Science.
In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Find the number of students who play neither?
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study English only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study at least one of the three languages
Let S = {x | x is a positive multiple of 3 less than 100}
P = {x | x is a prime number less than 20}. Then n(S) + n(P) is ______.
