Advertisements
Advertisements
प्रश्न
Let S = set of points inside the square, T = the set of points inside the triangle and C = the set of points inside the circle. If the triangle and circle intersect each other and are contained in a square. Then ______.
विकल्प
S ∩ T ∩ C = Φ
S ∪ T ∪ C = C
S ∪ T ∪ C = S
S ∪ T = S ∩ C
उत्तर
Let S = set of points inside the square, T = the set of points inside the triangle and C = the set of points inside the circle. If the triangle and circle intersect each other and are contained in a square. Then S ∪ T ∪ C = S.
Explanation:
The given conditions of the question may be represented by the following Venn diagram.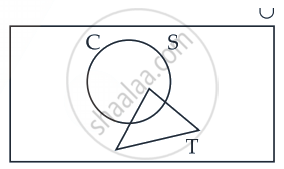
From the given Venn diagram, we clearly conclude that S ∪ T ∪ C = S
APPEARS IN
संबंधित प्रश्न
Identify whether the following is set or not? Justify your answer.
The collection of ten most talented writers of India.
Write the following set in roster form:
B = {x : x is a natural number less than 6}
Write the following set in the set-builder form:
{2, 4, 6, …}
Match each of the set on the left in the roster form with the same set on the right described in set-builder form:
| (i) | {1, 2, 3, 6} | (a) | {x : x is a prime number and a divisor of 6} |
| (ii) | {2, 3} | (b) | {x : x is an odd natural number less than 10} |
| (iii) | {M, A, T, H, E, I, C, S} | (c) | {x : x is natural number and divisor of 6} |
| (iv) | {1, 3, 5, 7, 9} | (d) | {x : x is a letter of the word MATHEMATICS} |
Which of the following collection are sets? Justify your answer:
The collection of difficult topics in mathematics.
If A = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10], then insert the appropriate symbol ∈ or ∉ in each of the following blank space:
0 ...... A
Describe the following set in Roster form:
The set of all letters in the word 'Trigonometry'
Describe the following sets in set-builder form:
{1, 4, 9, 16, ..., 100}
List all the elements of the following set:
D = {x : x is a vowel in the word "EQUATION"}
List all the elements of the following set:
F = {x : x is a letter of the word "MISSISSIPPI"}
Which of the following statemen are correct?
Write a correct form of each of the incorrect statement.
\[\left\{ a, b \right\} \subset \left\{ a, \left\{ b, c \right\} \right\}\]
Let A = {a, b, {c, d}, e}. Which of the following statements are false and why?
\[\left\{ a, b, e \right\} \in A\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\left\{ a, b, c \right\} \subset A\]
Let A = {a, b, {c, d}, e}. Which of the following statement are false and why?
\[\phi \in A\]
Let A = {{1, 2, 3}, {4, 5}, {6, 7, 8}}. Determine which of the following is true or false:
\[\phi \in A\]
Let \[A = \left\{ \phi, \left\{ \phi \right\}, 1, \left\{ 1, \phi \right\}, 2 \right\}\] Which of the following are true? \[\left\{ 1 \right\} \in A\]
Write down all possible proper subsets each of the following set:
{1, 2},
What is the total number of proper subsets of a set consisting of n elements?
Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 6, 8} and B = {2, 3, 5, 7}. Verify that \[\left( A \cap B \right)' = A' \cup B'\]
Let A = {1, 2, 3, 4, 5, 6}. Insert the appropriate symbol ∈ or ∉ in the blank space:
2 _____ A
If A = {x/6x2 + x – 15 = 0}, B = {x/2x2 – 5x – 3 = 0}, C = {x/2x2 – x – 3 = 0} then find (A ∩ B ∩ C)
In a class of 200 students who appeared in certain examinations, 35 students failed in CET, 40 in NEET and 40 in JEE, 20 failed in CET and NEET, 17 in NEET and JEE, 15 in CET and JEE, and 5 failed in all three examinations. Find how many students, did not fail in any examination.
Write the following interval in Set-Builder form:
[6, 12]
Write the following sets in the roaster form.
C = {x : x2 + 7x – 8 = 0, x ∈ R}
Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed in English and Mathematics but not in Science.
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study French only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study English only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study Sanskrit only
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4 French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who study at least one of the three languages
